Zestaw użytkownika nr 4316_4307

Zestaw użytkownika
nr 4316_4307

Zadanie 1

Reszta z dzielenia wielomianu 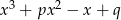3 2 x + px − x + q przez trójmian 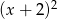2 (x + 2) wynosi 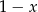1 − x . Wyznacz pierwiastki tego wielomianu.

Zadanie 2

Liczba 2 jest miejscem zerowym wielomianu 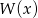W (x) . Wyznacz resztę z dzielenia tego wielomianu przez wielomian 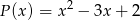P (x) = x 2 − 3x + 2 jeśli wiadomo, że w wyniku dzielenia wielomianu 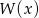W (x ) przez dwumian 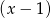(x − 1) otrzymujemy resztę 5.

Zadanie 3

Dany jest wielomian 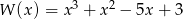3 2 W (x) = x + x − 5x + 3 .

  • Oblicz resztę z dzielenia tego wielomianu przez dwumian (x + 1) .
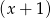  • Oblicz miejsca zerowe tego wielomianu.
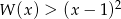  • Rozwiąż nierówność W (x) > (x − 1)2 .
Zadanie 4

Wielomian 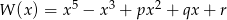5 3 2 W (x) = x − x + px + qx + r jest podzielny przez wielomian 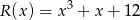R (x) = x 3 + x + 12 . Wyznacz liczby 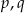p ,q i r .

Zadanie 5

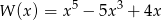Uzasadnij, że dla każdej liczby naturalnej x wartość wielomianu W (x) = x5 − 5x3 + 4x jest liczbą podzielną przez 120.

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze