Zestaw użytkownika nr 4322_5788
Funkcja kwadratowa cz. 1Grupa ISuma punktów: 24
Punkty 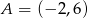 i
i 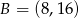 należą do wykresu funkcji
należą do wykresu funkcji 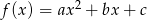 . Funkcja
. Funkcja 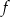 ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej
ma dwa miejsca zerowe, a wierzchołek paraboli będącej jej wykresem należy do prostej 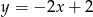 . Znajdź wzór tej funkcji.
. Znajdź wzór tej funkcji.
Znajdź wzór funkcji kwadratowej 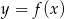 , której wykresem jest parabola o wierzchołku
, której wykresem jest parabola o wierzchołku 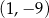 przechodząca przez punkt o współrzędnych
przechodząca przez punkt o współrzędnych 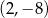 . Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
. Otrzymaną funkcję przedstaw w postaci kanonicznej. Oblicz jej miejsca zerowe i naszkicuj wykres.
Rozwiąż równanie 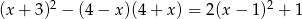 .
.
Funkcja kwadratowa 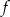 jest określona wzorem
jest określona wzorem 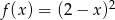 .
.
- Wyznacz najmniejszą i największą wartość funkcji
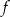 w przedziale
w przedziale 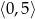 .
. - Rozwiąż nierówność
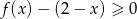 .
.
Większa część uczniów klasy liczącej 31 osób zachorowała na grypę. Zdrowi uczniowie postanowili wysłać chorym kolegom kartki z pozdrowieniami. Wiedząc, że każdy zdrowy uczeń wysłał do każdego chorego kolegi kartkę oraz, że liczba wysłanych kartek była największa z możliwych, oblicz ilu uczniów zachorowało na grypę.

