Zestaw użytkownika nr 4386_2655

FUNKCJA WYMIERNAPOZIOM ROZSZERZONY17 Grudnia 2012Czas pracy: 90 min.Suma punktów: 60

Zadanie 1

(5 pkt)

Dla jakich wartości parametru 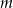dziedziną funkcji 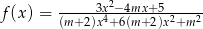-----3x2−4mx+-5----- f(x ) = (m+2)x4+6(m+ 2)x2+m 2 jest zbiór liczb rzeczywistych?

Zadanie 2

(5 pkt)

Uprość wyrażenie 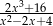-2x3+-16-- x2−2x+4 .

Zadanie 3

(5 pkt)

Wyznacz dziedzinę funkcji 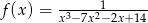------1------ f(x ) = x3−7x2−2x+14 .

Zadanie 4

(5 pkt)

Uzasadnij, że funkcja 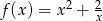2 2 f (x) = x + x przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.

Zadanie 5

(5 pkt)

Wyznacz wszystkie całkowite wartości 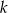, dla których funkcja 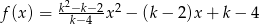2 f (x) = k-−k−k−42-x2 − (k− 2 )x+ k− 4 osiąga minimum i ma dwa różne miejsca zerowe.

Zadanie 6

(5 pkt)

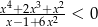Rozwiąż nierówność x4+-2x3+x-2 x− 1+ 6x2 < 0 .

Zadanie 7

(5 pkt)

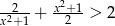Rozwiąż nierówność --2- x2+-1 x2+ 1 + 2 > 2 .

Zadanie 8

(5 pkt)

Rozwiąż równanie 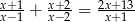x+1- x+-2 2x+-13 x−1 + x− 2 = x+ 1 .

Zadanie 9

(5 pkt)

Funkcja 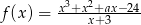x3+x-2+ax−24- f(x) = x+3 ma miejsce zerowe równe (-2). Wyznacz:

wartość parametru ;
pozostałe miejsca zerowe funkcji;
zbiór tych argumentów, dla których funkcja przyjmuje wartości nieujemne.

Zadanie 10

(5 pkt)

Określ liczbę rozwiązań równania 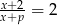x+2- x+p = 2 w zależności od wartości parametru .

Zadanie 11

(5 pkt)

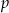Funkcja 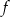określona jest wzorem 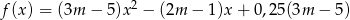2 f(x ) = (3m − 5 )x − (2m − 1)x + 0 ,25(3m − 5) . Wyznacz te wartości parametru 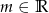m ∈ R , dla których najmniejsza wartość funkcji 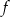jest liczbą dodatnią.

Zadanie 12

(5 pkt)

Określ dziedzinę funkcji 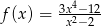3x4−-12- f(x) = x2− 2 i sprowadź jej wzór do najprostszej postaci. Naszkicuj jej wykres i podaj jej zbiór wartości.

Rozwiąż on-line Arkusz Wersja PDF