Zestaw użytkownika nr 4387_2340
Ciąg geometrycznySuma punktów: 30
Ciągiem geometrycznym jest ciąg określony wzorem
A) 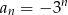 B)
B) 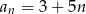 C)
C) 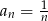 D)
D) 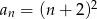
Trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) 16 B) -16 C) 8 D) -8
Dany jest ciąg geometryczny 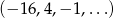 . Wyraz ogólny tego ciągu to
. Wyraz ogólny tego ciągu to
A) 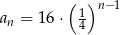 B)
B) 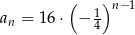 C)
C) 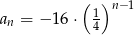 D)
D) 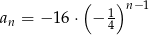
Dany jest ciąg geometryczny o wyrazie ogólnym 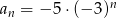 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) -135 B) -45 C) 45 D) 135
W ciągu geometrycznym 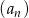 dane są
dane są 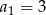 i
i 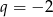 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 255 B) -255 C) 257 D) -257
W malejącym ciągu geometrycznym 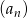 mamy:
mamy: 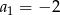 i
i 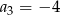 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -2 B) 2 C) 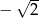 D)
D) 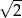
W ciągu geometrycznym 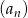 dane są:
dane są: 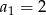 i
i 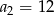 . Wtedy
. Wtedy
A) 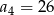 B)
B) 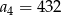 C)
C) 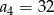 D)
D) 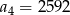
Dany jest ciąg geometryczny o wyrazie ogólnym 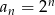 , dla
, dla 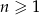 . Liczba wyrazów tego ciągu mniejszych od 64 jest równa
. Liczba wyrazów tego ciągu mniejszych od 64 jest równa
A) 6 B) 5 C) 4 D) 3
Liczby 2,6 są dwoma początkowymi wyrazami ciągu geometrycznego. Do wyrazów tego ciągu nie należy liczba
A) 162 B) 54 C) 18 D) 9
Pierwszy wyraz ciągu geometrycznego jest równy 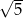 , a iloraz
, a iloraz 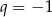 . Suma 1001 wyrazów tego ciągu jest równa
. Suma 1001 wyrazów tego ciągu jest równa
A) 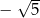 B) 0 C)
B) 0 C) 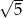 D)
D) 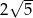
W ciągu geometrycznym 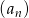 dane są:
dane są: 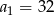 i
i 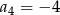 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 12 B) 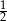 C)
C) 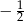 D) -12
D) -12
Liczby 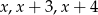 tworzą ciąg geometryczny. Wynika stąd, że
tworzą ciąg geometryczny. Wynika stąd, że
A) 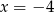 B)
B) 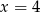 C)
C) 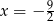 D)
D) 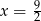
- Sprawdź, czy ciąg o wyrazach 2, 6, 18, 36 jest geometryczny.
- Wyznacz cztery początkowe wyrazy ciągu geometrycznego, jeśli:
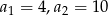 .
. - Jaką liczbą musi być
 , aby liczby:
, aby liczby: 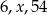 tworzyły ciąg geometryczny.
tworzyły ciąg geometryczny.
Uzasadnij, że ciąg określony wzorem 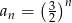 jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
jest ciągiem geometrycznym. Wyznacz iloraz tego ciągu.
Iloraz ciągu geometrycznego 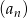 jest równy
jest równy 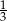 , a suma jego pięciu początkowych wyrazów wynosi -605. Znajdź pierwszy wyraz ciągu
, a suma jego pięciu początkowych wyrazów wynosi -605. Znajdź pierwszy wyraz ciągu 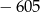 oraz określ jego monotoniczność.
oraz określ jego monotoniczność.
Oblicz
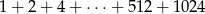 ,
, 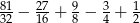 .
.
Oblicz pierwszy wyraz i iloraz ciągu geometrycznego 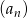 , wiedząc, że
, wiedząc, że 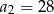 i
i 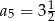 . Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.
. Oblicz sumę dziesięciu początkowych wyrazów tego ciągu.

