Zestaw użytkownika nr 4422_4340
Sesja egzaminacyjna czerwiec 2011I LO7 Czerwca 2011Czas pracy: 30 min.Suma punktów: 20
Kąt  jest ostry
jest ostry 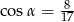 . Oblicz
. Oblicz 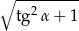 .
.
Kąt  jest kątem ostrym i
jest kątem ostrym i 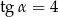 . Wyznacz sinus i cosinus tego kąta.
. Wyznacz sinus i cosinus tego kąta.
Wyznacz długości boków oraz miary kątów trójkąta prostokątnego jeżeli 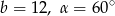 .
.
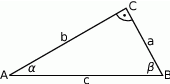
W trójkącie prostokątnym naprzeciw kąta ostrego  leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
leży przyprostokątna długości 3 cm. Druga przyprostokątna ma długość 6 cm. Zatem
A) 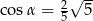 B)
B) 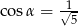 C)
C) 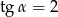 D)
D) 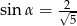
Trójkąt prostokątny ma boki długości 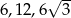 i kąty ostre
i kąty ostre 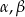 . Kąt
. Kąt 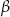 leży naprzeciw boku długości
leży naprzeciw boku długości 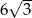 . Zatem
. Zatem
A) 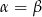 B)
B) 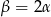 C)
C) 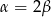 D)
D) 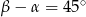
Dany jest trójkąt prostokątny (patrz rysunek).
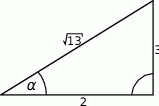
Wartość wyrażenia 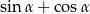 wynosi
wynosi
A) 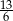 B) 1 C)
B) 1 C) 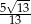 D)
D) 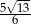
Wskaż funkcję, która nie przyjmuje wartości ujemnych
A) 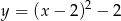 B)
B) 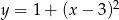 C)
C) 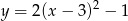 D)
D) 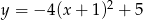
Funkcja 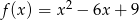 dla argumentu
dla argumentu 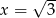 przyjmuje wartość
przyjmuje wartość
A) 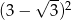 B) -36 C)
B) -36 C) 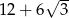 D)
D) 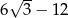
Funkcja 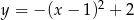 jest rosnąca w przedziale:
jest rosnąca w przedziale:
A) 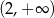 B)
B) 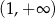 C)
C) 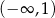 D)
D) 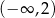
Dana jest funkcja 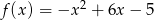 .
.
- Narysuj parabolę, która jest wykresem funkcji
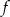 i zaznacz na rysunku współrzędne jej wierzchołka oraz punktów przecięcia paraboli z osiami układu współrzędnych.
i zaznacz na rysunku współrzędne jej wierzchołka oraz punktów przecięcia paraboli z osiami układu współrzędnych. - Odczytaj z wykresu zbiór wartości funkcji
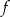 .
. - Rozwiąż nierówność
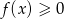 .
.