Zestaw użytkownika nr 4479_3897
Zestaw użytkownika
nr 4479_3897
O zdarzeniach 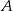 i
i 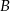 wiadomo, że
wiadomo, że 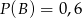 ,
, 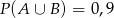 oraz
oraz 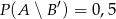 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 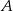 .
.
Wiadomo, że zdarzenia 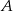 i
i 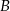 są niezależne oraz
są niezależne oraz 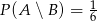 ,
, 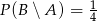 . Oblicz
. Oblicz 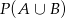 .
.
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia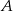 – na każdej kostce wypadła nieparzysta liczba oczek,
– na każdej kostce wypadła nieparzysta liczba oczek,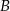 – suma wyrzuconych oczek jest nie mniejsza niż 8.
– suma wyrzuconych oczek jest nie mniejsza niż 8.
Oblicz prawdopodobieństwo zdarzenia 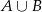 .
.
Ze zbioru 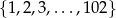 losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
losujemy 2 różne liczby. Jakie jest prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3?
Dane są zbiory liczb całkowitych: 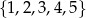 i
i 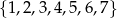 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
Ze zbioru 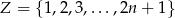 , gdzie
, gdzie 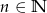 wylosowano równocześnie dwie liczby. Wyznacz
wylosowano równocześnie dwie liczby. Wyznacz  , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od
, tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 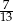 .
.

