Zestaw użytkownika nr 4533_3873
FunkcjeCzas pracy: 45 min.Suma punktów: 16
Funkcja liniowa, której wykres jest równoległy do wykresu funkcji 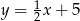 ma wzór:
ma wzór:
A) 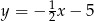 B)
B) 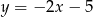 C)
C) 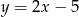 D)
D) 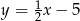
Funkcja 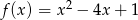 jest rosnąca w przedziale
jest rosnąca w przedziale
A) 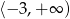 B)
B) 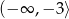 C)
C) 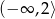 D)
D) 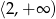
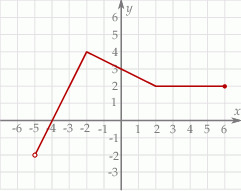
Na rysunku przedstawiony jest wykres funkcji 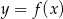 . Rozwiązaniem nierówności
. Rozwiązaniem nierówności 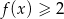 jest przedział
jest przedział
A) 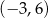 B)
B) 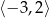 C)
C) 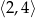 D)
D) 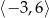
Do wykresu funkcji liniowej 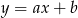 należą punkty
należą punkty 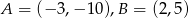 . Wynika stąd, że
. Wynika stąd, że
A) 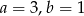 B)
B) 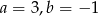 C)
C) 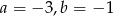 D)
D) 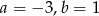
Zbiór liczb rzeczywistych jest dziedziną funkcji:
A) 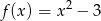 B)
B) 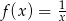 C)
C) 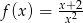 D)
D) 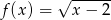
Punkt 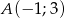 należy do wykresu funkcji:
należy do wykresu funkcji:
A) 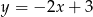 B)
B) 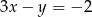 C)
C) 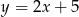 D)
D) 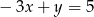
Dana jest funkcja 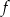 określona wzorem
określona wzorem 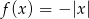 . Ta funkcja przyjmuje wartości ujemne dla
. Ta funkcja przyjmuje wartości ujemne dla
A) 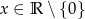 B)
B) 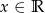 C)
C) 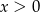 D)
D) 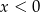
Na którym rysunku przedstawiono wykres funkcji liniowej 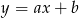 takiej, że
takiej, że 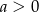 i
i 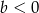 ?
?
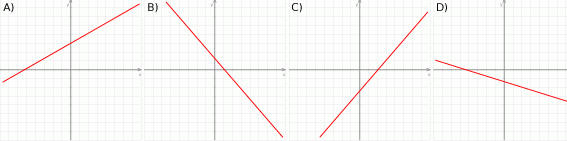
Wyznacz miejsca zerowe funkcji
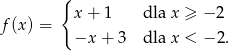
Określ dziedzinę funkcji  .
.
Miejscami zerowymi funkcji kwadratowej 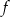 są liczby (-6) oraz 1. Oblicz wartość wyrażenia
są liczby (-6) oraz 1. Oblicz wartość wyrażenia 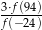 .
.
Dany jest trójmian kwadratowy 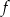 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 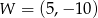 . Oblicz
. Oblicz 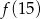 .
.

