Zestaw użytkownika nr 4603_9590

Zestaw użytkownika
nr 4603_9590

Zadanie 1
(5 pkt)

Podstawą prostopadłościanu jest kwadrat o boku długości 4, a wysokość prostopadłościanu jest równa 8. Połączono odcinkami środki trzech krawędzi prostopadłościanu, z których żadne dwie nie leżą w jednej płaszczyźnie, i otrzymano trójkąt 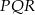PQR

  • Oblicz długości boków trójkąta P QR .
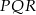  • Wyznacz miary kątów trójkąta P QR .
Zadanie 2
(5 pkt)

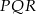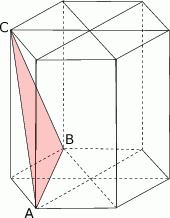
W graniastosłupie prawidłowym sześciokątnym płaszczyzna 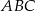ABC zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 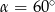α = 60∘ . Pole przekroju graniastosłupa tą płaszczyzną równa się 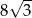8√ 3- . Zaznacz na poniższym rysunku kąt α . Oblicz objętość tego graniastosłupa.

PIC

Zadanie 3
(5 pkt)

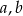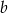Trzy wychodzące z jednego wierzchołka krawędzie równoległościanu są równe a,b i c . Krawędzie a i b są prostopadłe, a krawędź c tworzy z każdą z nich kąt ostry α . Oblicz objętość równoległościanu.

Zadanie 4
(5 pkt)

Oblicz objętość i pole powierzchni graniastosłupa, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze 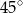45∘ .

Zadanie 5
(5 pkt)

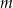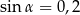W graniastosłupie czworokątnym prawidłowym przekątna o długości m jest nachylona do płaszczyzny podstawy pod kątem α . Wiadomo, że sin α = 0,2 . Wyznacz objętość tego graniastosłupa.

Rozwiąż on-line Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze