Zestaw użytkownika nr 4703_3848
Zestaw użytkownika
nr 4703_3848
Rozłóż na czynniki drugiego stopnia wielomian 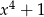 .
.
Rozłóż wielomian 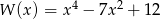 na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
na czynniki liniowe. Podaj niewymierne pierwiastki tego wielomianu.
Zbadaj, na podstawie definicji, monotoniczność funkcji 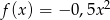 w zbiorze
w zbiorze 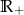 .
.
Dana jest funkcja 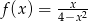 , gdzie
, gdzie 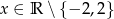 . Wykaż, że zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych.
. Wykaż, że zbiorem wartości tej funkcji jest zbiór liczb rzeczywistych.
Określ dziedzinę funkcji 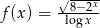 .
.
Wyznacz zbiór wartości funkcji
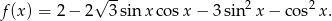
Rozłóż wielomian 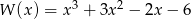 na czynniki liniowe.
na czynniki liniowe.
Wyznacz wzór funkcji liniowej 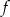 wiedząc, że zbiorem rozwiązań nierówności
wiedząc, że zbiorem rozwiązań nierówności 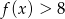 jest przedział
jest przedział 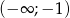 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 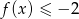 jest przedział
jest przedział 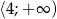 .
.
Dana jest funkcja 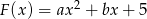 . Wyznacz
. Wyznacz  i
i 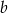 wiedząc, że
wiedząc, że 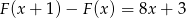 .
.
Uzasadnij, że funkcja 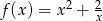 przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
przyjmuje dla dodatnich argumentów wartości nie mniejsze niż 3.
Wiedząc, że 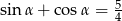 , oblicz
, oblicz 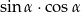 .
.
Kąt  jest ostry oraz
jest ostry oraz 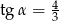 . Oblicz
. Oblicz 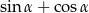 .
.
Dla jakich wartości parametru 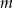 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
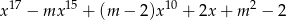
przez dwumian 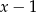 jest równa 3?
jest równa 3?
Wyznacz największą wartość funkcji 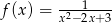 .
.
Wyznacz dziedzinę i najmniejszą wartość funkcji 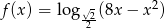 .
.
Wyznacz dziedzinę funkcji 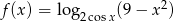 i zapisz ją w postaci sumy przedziałów liczbowych.
i zapisz ją w postaci sumy przedziałów liczbowych.
Wielomian 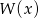 przy dzieleniu przez dwumiany
przy dzieleniu przez dwumiany 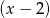 ,
, 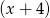 daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu
daje reszty odpowiednio równe -3 oraz -51. Wyznacz resztę z dzielenia wielomianu 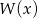 przez wielomian
przez wielomian 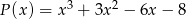 , wiedząc, że liczba -1 jest miejscem zerowym wielomianu
, wiedząc, że liczba -1 jest miejscem zerowym wielomianu 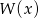 .
.
Jedynym miejscem zerowym funkcji kwadratowej 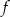 jest liczba 2. Wykres funkcji
jest liczba 2. Wykres funkcji 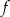 przecina oś
przecina oś 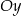 w punkcie o współrzędnych
w punkcie o współrzędnych 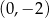 . Wyznacz wzór tej funkcji w postaci ogólnej.
. Wyznacz wzór tej funkcji w postaci ogólnej.
Wyznacz wszystkie wartości parametru 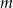 , dla których funkcja
, dla których funkcja 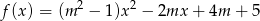 jest rosnąca w przedziale
jest rosnąca w przedziale 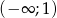 i malejąca w przedziale
i malejąca w przedziale 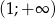 .
.
Wielomian 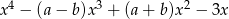 jest podzielny przez wielomian
jest podzielny przez wielomian 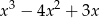 . Oblicz
. Oblicz  i
i 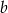 .
.

