Zestaw użytkownika nr 4826_1987
Zestaw użytkownika
nr 4826_1987
Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.
Oblicz pole powierzchni całkowitej i objętość prostopadłościanu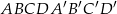 
, w którym krawędź 
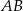ma długość 10 cm i tworzy z przekątną 
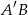ściany bocznej kąt 
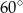, a krawędź 
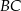jest o cztery centymetry krótsza od krawędzi 
.
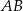Mrówka przeszła po powierzchni sześcianu z wierzchołka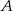 
do wierzchołka będącego drugim końcem przekątnej wychodzącej z wierzchołka 
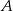, przy czym była to droga najkrótsza. Narysuj siatkę sześcianu i oblicz odległość, jaką pokonała mrówka, jeżeli krawędź sześcianu ma długość 
.
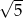Oblicz objętość i pole powierzchni graniastosłupa, którego podstawą jest romb o przekątnych długości 6 cm i 8 cm, którego przekątna ściany bocznej tworzy z krawędzią podstawy kąt o mierze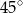 
.
Pole powierzchni czworościanu foremnego jest równe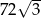 
. Oblicz długość krawędzi tego czworościanu.
W graniastosłupie prawidłowym czworokątnym powierzchnia boczna po rozwinięciu jest kwadratem o polu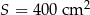 
. Oblicz objętość i pole powierzchni całkowitej tej bryły .
Oblicz pole powierzchni i objętość sześcianu, którego przekątna ma długość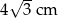 
.
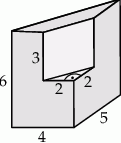
Bryła przedstawiona na poniższym rysunku powstała przez wycięcie z graniastosłupa prostego trójkątnego innego graniastosłupa prostego. Oblicz pole powierzchni i objętość tej bryły.
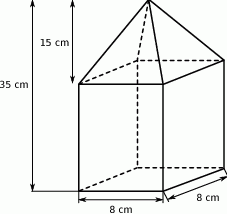
Oblicz objętość bryły, której kształt i wymiary przedstawiono na rysunku. Zapisz obliczenia.
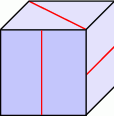
Popatrz na kostkę przedstawioną na rysunku. Wiadomo, że na każdej ścianie narysowany jest odcinek oraz że odcinki na przeciwległych ścianach są równoległe. Narysuj siatkę z której można skleić tę kostkę. Na każdej ścianie narysuj odpowiedni odcinek.
Z jednakowych sześciennych kostek, których krawędź ma długość 1, sklejono bryłę przedstawioną na rysunku.
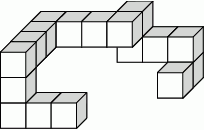
Ile kostek należy dokleić do tej bryły, aby otrzymać wypełniony kostkami sześcian?
Ile ścian bocznych ma graniastosłup o 14 wierzchołkach?
Wysokość prostopadłościanu o podstawie kwadratowej jest dwa razy dłuższa od krawędzi podstawy. Objętość prostopadłościanu jest równa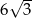 
. Wyznacz pole powierzchni całkowitej tego prostopadłościanu.
Graniastosłup prawidłowy czworokątny o krawędzi 4 cm i wysokości 3 cm przecięto płaszczyzną, która zawiera przekątne przeciwległych ścian bocznych. Jakie pole ma ten przekrój?
