Zestaw użytkownika nr 4830_2374

Zestaw użytkownika
nr 4830_2374

Zadanie 1

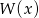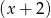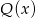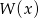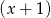W wyniku podzielenia wielomianu W (x) przez (x + 2) otrzymujemy iloraz Q (x) i resztę 0. Jeśli natomiast podzielimy wielomian W (x) przez (x + 1) , to otrzymamy iloraz 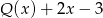Q (x)+ 2x − 3 i resztę 2.

  • Wyznacz wielomian W (x) .
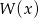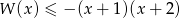  • Rozwiąż nierówność W (x) ≤ − (x + 1 )(x + 2) .
Zadanie 2

Wielomian 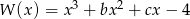3 2 W (x) = x + bx + cx− 4 jest podzielny przez trójmian kwadratowy 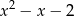x2 − x − 2 . Wyznacz współczynniki 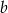b i c wielomianu W (x) .

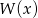Zadanie 3

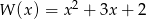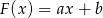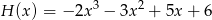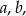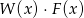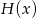Dane są wielomiany 2 W (x) = x + 3x+ 2 , F (x) = ax + b , H (x) = − 2x3 − 3x2 + 5x + 6 . Wyznacz współczynniki a,b, dla których wielomiany W (x) ⋅F(x ) oraz H (x ) są równe.

Zadanie 4

Dany jest wielomian 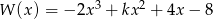3 2 W (x) = − 2x + kx + 4x − 8 .

  • Wyznacz wartość 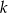k tak, aby reszta z dzielenia wielomianu W przez dwumian 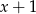x + 1 była równa -6.
  • Dla znalezionej wartości 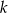k rozłóż wielomian na czynniki liniowe.
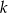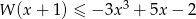  • Dla znalezionej wartości k rozwiąż nierówność W (x + 1) ≤ − 3x 3 + 5x − 2 .
Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze