/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 14 marca 2020 Czas pracy: 170 minut
Zadania zamknięte
Rozwiązaniem równania 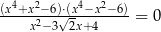 nie jest liczba
nie jest liczba
A) 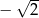 B)
B) 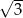 C)
C) 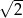 D)
D) 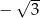
Wartość liczbowa wyrażenia 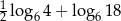 jest równa
jest równa
A) 2 B) 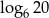 C) 6 D)
C) 6 D) 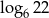
Stężenie roztworu kwasu siarkowego przez pierwszą godzinę pewnego eksperymentu było równe 25%. Na początku drugiej godziny eksperymentu stężenie zmalało o 5 punktów procentowych. Oznacza to, że stężenie tego roztworu kwasu siarkowego zmalało o
A) 5% B) 25% C) 20% D) 75%
Na rysunku 1. jest przedstawiony wykres funkcji 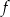 , a na rysunku 2. – wykres funkcji
, a na rysunku 2. – wykres funkcji 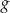 .
.
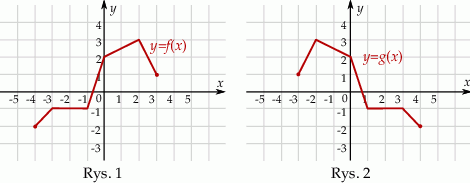
Funkcja 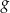 jest określona wzorem
jest określona wzorem
A) 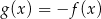 B)
B) 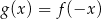 C)
C) 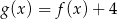 D)
D) 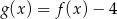
Suma współrzędnych wierzchołka paraboli 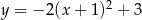 jest równa
jest równa
A) 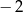 B) 2 C)
B) 2 C) 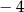 D) 4
D) 4
Miejscami zerowymi funkcji kwadratowej 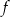 określonej wzorem
określonej wzorem 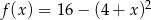 są liczby
są liczby
A) 0 oraz 4 B) 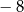 oraz 8 C) 0 oraz
oraz 8 C) 0 oraz 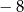 D)
D) 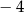 oraz 4
oraz 4
Miejscem zerowym funkcji liniowej 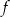 określonej wzorem
określonej wzorem 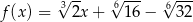 jest liczba
jest liczba
A) 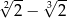 B)
B) 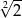 C)
C) 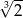 D)
D) 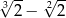
Układ równań 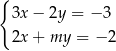 ma nieskończenie wiele rozwiązań dla
ma nieskończenie wiele rozwiązań dla
A) 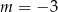 B)
B) 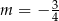 C)
C) 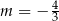 D)
D) 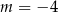
Wartość wyrażenia 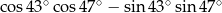 jest równa
jest równa
A) 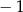 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
Który z podanych ciągów jest rosnącym ciągiem geometrycznym?
A) 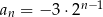 B)
B) 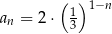 C)
C) 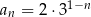 D)
D) 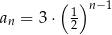
Liczbą mniejszą od 3 jest
A) 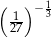 B)
B) 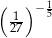 C)
C) 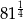 D)
D) 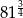
W ciągu arytmetycznym 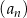 określonym dla
określonym dla 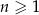 , średnia arytmetyczna wyrazów:
, średnia arytmetyczna wyrazów: 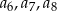 jest o 33 mniejsza od średniej arytmetycznej wyrazów
jest o 33 mniejsza od średniej arytmetycznej wyrazów 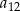 i
i 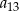 . Różnica tego ciągu jest równa
. Różnica tego ciągu jest równa
A) 6 B) 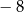 C)
C) 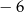 D) 8
D) 8
Sinus kąta rozwartego  jest równy
jest równy  . Wtedy
. Wtedy
A) 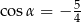 B)
B) 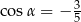 C)
C) 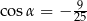 D)
D) 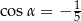
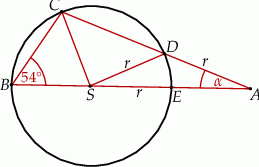
Punkty 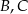 i
i 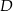 leżą na okręgu o środku
leżą na okręgu o środku 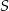 i promieniu
i promieniu  . Punkt
. Punkt 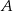 jest punktem wspólnym prostych
jest punktem wspólnym prostych 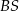 i
i 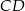 , a odcinki
, a odcinki 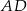 i
i 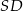 są równej długości. Miara kąta
są równej długości. Miara kąta 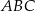 jest równa
jest równa 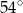 (zobacz rysunek). Wtedy
(zobacz rysunek). Wtedy
A) 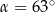 B)
B) 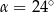 C)
C) 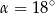 D)
D) 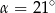
Dany jest trójkąt równoramienny 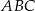 , w którym
, w którym 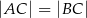 . Na podstawie
. Na podstawie 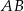 tego trójkąta leży punkt
tego trójkąta leży punkt 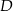 , taki że
, taki że 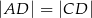 ,
, 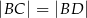 (zobacz rysunek).
(zobacz rysunek).
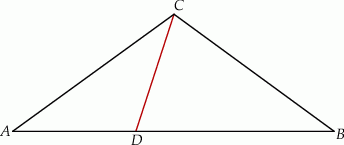
Wynika stąd, że kąt 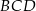 ma miarę
ma miarę
A) 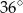 B)
B) 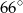 C)
C) 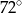 D)
D) 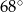
Okrąg, którego środkiem jest punkt 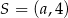 , jest styczny do osi
, jest styczny do osi 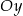 i do prostej o równaniu
i do prostej o równaniu 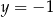 . Promień tego okręgu jest równy
. Promień tego okręgu jest równy
A) 3 B) 5 C) 2 D) 4
Odcinek o końcach 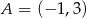 i
i 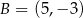 jest równoległy do prostej o równaniu
jest równoległy do prostej o równaniu
A) 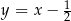 B)
B) 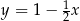 C)
C) 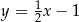 D)
D) 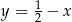
W układzie współrzędnych na płaszczyźnie dany jest odcinek 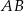 o końcach w punktach
o końcach w punktach 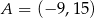 ,
, 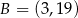 . Punkt
. Punkt 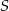 leży wewnątrz odcinka
leży wewnątrz odcinka 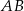 oraz
oraz 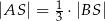 . Wówczas
. Wówczas
A) 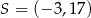 B)
B) 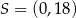 C)
C) 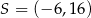 D)
D) 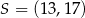
Punkt 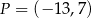 przekształcono w symetrii względem symetralnej odcinka o końcach
przekształcono w symetrii względem symetralnej odcinka o końcach 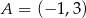 i
i 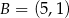 . W wyniku tego przekształcenia otrzymano punkt
. W wyniku tego przekształcenia otrzymano punkt 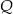 . Zatem długość odcinka
. Zatem długość odcinka 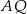 jest równa
jest równa
A) 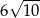 B)
B) 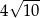 C)
C) 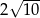 D)
D) 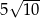
Walec i stożek mają równe promienie podstaw, a wysokość walca jest trzy razy dłuższa niż wysokość stożka. Stosunek objętości walca do objętości stożka jest równa
A) 9 B) 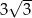 C) 3 D) 27
C) 3 D) 27
Bloczek betonowy fundamentowy ma kształt prostopadłościanu o wymiarach 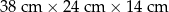 (zobacz rysunek).
(zobacz rysunek).
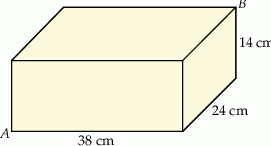
Przekątna 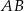 tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
tego prostopadłościanu jest – z dokładnością do 0,01 dm – równa
A) 4,71 dm B) 4,49 dm C) 4,05 dm D) 4,7 dm
Wszystkich liczb naturalnych czterocyfrowych nieparzystych, w których występują wyłącznie cyfry 1, 2, 3, jest
A) 54 B) 81 C) 8 D) 27
Średnia arytmetyczna dziesięciu liczb naturalnych: 21, 11, 5,  ,
,  ,
,  ,
,  , 24, 18, 15 jest równa 13. Mediana tych liczb jest równa
, 24, 18, 15 jest równa 13. Mediana tych liczb jest równa
A) 11 B) 9 C) 10 D) 
Przekrój osiowy stożka jest trójkątem rozwartokątnym o polu 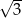 . Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
. Jeżeli tworząca tego stożka ma długość 2, to jego objętość jest równa
A) 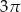 B)
B) 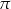 C)
C) 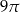 D)
D) 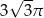
Rzucamy czterokrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że suma oczek wyrzuconych w czterech rzutach jest różna od 23 jest równe
A) 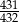 B)
B) 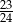 C)
C) 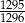 D)
D) 
Zadania otwarte
Wyznacz wszystkie liczby pierwsze spełniające nierówność
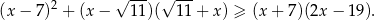
Wyznacz wszystkie liczby rzeczywiste  , które spełniają warunek:
, które spełniają warunek: 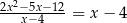 .
.
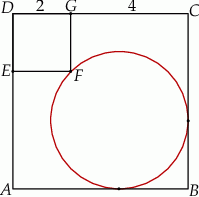
Na rysunku przedstawiono dwa kwadraty: 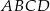 i
i 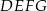 , przy czym punkty
, przy czym punkty 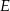 i
i 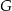 należą do odcinków
należą do odcinków 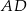 i
i 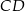 odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu
odpowiednio. Przedstawiono również okrąg, który jest styczny do dwóch boków kwadratu 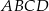 i przechodzi przez punkt
i przechodzi przez punkt 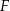 . Wykaż, że jeżeli
. Wykaż, że jeżeli 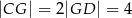 , to promień okręgu jest równy
, to promień okręgu jest równy 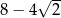 .
.
Wykaż, że dla dowolnej liczby 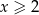 prawdziwa jest nierówność
prawdziwa jest nierówność 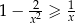 .
.
W ciągu geometrycznym przez 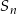 oznaczamy sumę
oznaczamy sumę  początkowych wyrazów tego ciągu, dla liczb naturalnych
początkowych wyrazów tego ciągu, dla liczb naturalnych 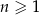 . Wiadomo, że dla pewnego ciągu geometrycznego:
. Wiadomo, że dla pewnego ciągu geometrycznego: 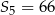 i
i 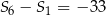 . Wyznacz iloraz i ósmy wyraz tego ciągu.
. Wyznacz iloraz i ósmy wyraz tego ciągu.
Odchylenie standardowe liczb: 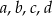 jest równe 0,1. Oblicz odchylenie standardowe danych:
jest równe 0,1. Oblicz odchylenie standardowe danych: 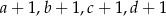 .
.
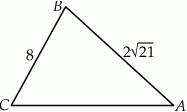
Dany jest trójkąt 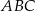 , w którym
, w którym 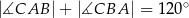 . Ponadto wiadomo, że
. Ponadto wiadomo, że 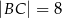 i
i 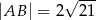 (zobacz rysunek). Oblicz długość trzeciego boku trójkąta
(zobacz rysunek). Oblicz długość trzeciego boku trójkąta 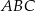 .
.
Wyznacz środek okręgu przechodzącego przez punkty 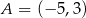 i
i 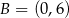 , którego środek leży na prostej o równaniu
, którego środek leży na prostej o równaniu 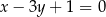 .
.
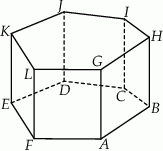
Dany jest graniastosłup prosty o podstawie sześciokątnej 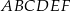 (zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta
(zobacz rysunek). Każda ze ścian bocznych tego graniastosłupa jest kwadratem o polu o 25% mniejszym niż pole sześciokąta 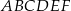 . Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.
. Pole powierzchni całkowitej tego graniastosłupa jest równe 156. Oblicz jego objętość.