/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2019/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 23 marca 2019 Czas pracy: 100 minut
Poniżej zamieszczono fragment etykiety z sałatki z kurczakiem o masie 250 g.
| Wartość odżywcza | w 100 g |
| energia | 570 kJ/137 kcal |
| tłuszcz w tym kwasy nasycone | 9,5 g 1,6 g |
| węglowodany w tym cukry | 4,6 g 3,3 g |
| błonnik | 2,6 g |
| białko | 7,0 g |
| sól | 0,102 g |
| wapń | 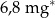 |
| potas | 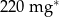 |
 1 mg=0,001 g
1 mg=0,001 g
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Zjedzenie całej sałatki dostarcza organizmowi około A/B potasu.
A) 440 mg B) 550 mg
Zjedzenie całej sałatki dostarcza organizmowi C/D razy więcej soli niż wapnia.
C) 15 D) 150
Ania pomyślała o pewnej liczbie dodatniej. Dodała do niej 96 i wynik potroiła. Okazało się, że otrzymana w ten sposób liczba jest o 400% większa od liczby, o której pomyślała Ania. O jakiej liczbie pomyślała Ania?
Wybierz odpowiedź spośród podanych.
A) 72 B) 288 C) 144 D) 48
Wujek Kasi odbył podróż pociągiem z Krakowa do Koszalina. W tabeli przedstawiono niektóre dane dotyczące tej podróży: czasy odjazdu, przyjazdu oraz czas na przesiadkę.
| Kraków | Warszawa | Przes. | Warszawa | Gdynia | Przes. | Gdynia | Koszalin |
| 16:50 | 19:14 | 11 min. | 19:25 | 127 min. | 0:58 | 3:32 |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wujek Kasi przyjechał do Gdyni o godz. 22:45. | P | F |
| Cała podróż z Krakowa do Koszalina trwała 10 godzin i 42 minuty. | P | F |
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli liczba dzieli się przez 144 i 96, to dzieli się też przez 576. | P | F |
| Jeżeli liczba jest dzielnikiem 144 i 96, to liczba ta jest dzielnikiem 48. | P | F |
Kwadrat 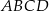 podzielono na 16 identycznych kwadratów (zobacz rysunek).
podzielono na 16 identycznych kwadratów (zobacz rysunek).
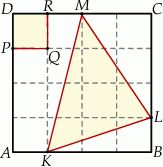
Jakim procentem pola kwadratu 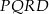 jest pole trójkąta
jest pole trójkąta 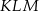 ? Wybierz odpowiedź spośród podanych.
? Wybierz odpowiedź spośród podanych.
A) 650% B) 600% C) 550% D) 500%
Średnia prędkość poruszania się mrówki to 50 centymetrów na minutę. Średnia prędkość biegnącego słonia to 39 kilometrów na godzinę.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Średnia prędkość biegnącego słonia jest 1300 razy większa od średniej prędkości mrówki. | P | F |
| W ciągu jednej godziny mrówka pokonuje dystans 30 metrów. | P | F |
Samochód taty Karola spala średnio 8 litrów benzyny na 100 km. W czasie ferii zimowych tata Karola planuje wyjazd na narty do Austrii – łącznie planuje przejechać około 1850 km i planuje, że za litr benzyny będzie płacił 1,4 euro.
Dokończ zdanie. Wybierz odpowiedź spośród podanych.
Orientacyjny koszt zakupu benzyny podczas wyjazdu na narty będzie równy
A) 25,9 euro B) 207 euro C) 2072 euro D) 185 euro
Krawędź sześcianu ma długość 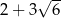 .
.
Uzupełnij poniższe zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Suma długości wszystkich krawędzi sześcianu jest równa A/B .
A) 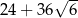 B)
B) 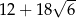
Pole powierzchni jednej ściany sześcianu jest równe C/D .
C) 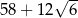 D)
D) 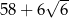
Informacja do zadań 9 i 10
Punkt kratowy to miejsce przecięcia się linii kwadratowej siatki. Pole wielokąta, którego wierzchołki znajdują się w punktach kratowych kwadratowej siatki na płaszczyźnie, można obliczyć ze wzoru Picka:
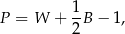
gdzie 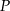 oznacza pole wielokąta,
oznacza pole wielokąta, 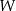 – liczbę punktów kratowych leżących wewnątrz wielokąta, a
– liczbę punktów kratowych leżących wewnątrz wielokąta, a 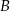 – liczbę punktów kratowych leżących na brzegu tego wielokąta.
– liczbę punktów kratowych leżących na brzegu tego wielokąta.
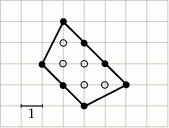
W wielokącie przedstawionym na rysunku 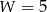 oraz
oraz 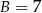 , zatem
, zatem 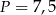 .
.
Wewnątrz pewnego wielokąta znajduje się 6 razy mniej punktów kratowych, niż na jego brzegu.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Pole tego wielokąta może być równe
A) 2018 B) 2019 C) 2020 D) 2021
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba punktów kratowych leżących na brzegu wielokąta o polu 35 może być równa
A) 57 B) 74 C) 37 D) 42
Do gry planszowej używane są dwa bączki o kształtach przedstawionych na rysunkach. Każdy bączek po zatrzymaniu na jednym boku wielokąta wskazuje liczbę umieszczoną na jego tarczy. Na rysunku I bączek ma kształt siedmiokąta foremnego z zaznaczonymi liczbami od 1 do 7. Na rysunku II bączek ma kształt sześciokąta foremnego z zaznaczonymi liczbami od 1 do 6.
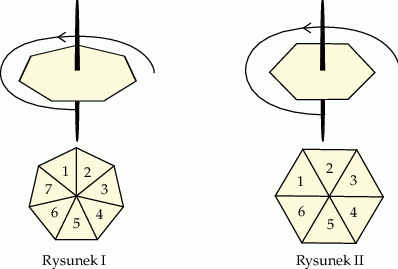
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Prawdopodobieństwo otrzymania liczby pierwszej na bączku z rysunku I jest większe niż 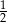 | P | F |
| Uzyskanie liczby parzystej na bączku z rysunku I jest tak samo prawdopodobne, jak uzyskanie liczby nieparzystej na bączku z rysunku II. | P | F |
Liczby naturalne od 1 do 8 umieszczono w wierzchołkach sześcianu w ten sposób, że w żadnych dwóch wierzchołkach nie umieszczono tej samej liczby. Następnie na każdej krawędzi sześcianu umieszczono sumę liczb, które znajdują się na końcach tej krawędzi, a na środku każdej ściany umieszczono sumę liczb, które znajdują w wierzchołkach tej ściany.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Suma wszystkich liczb umieszczonych na krawędziach sześcianu jest równa 72. | P | F |
| Suma wszystkich liczb umieszczonych w środkach ścian sześcianu jest równa 144. | P | F |
Punkt 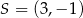 jest środkiem odcinka
jest środkiem odcinka 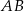 , w którym
, w którym 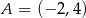 .
.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Punkt 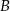 ma współrzędne
ma współrzędne
A) 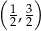 B)
B) 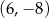 C)
C) 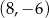 D)
D) 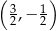
W równoległoboku 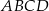 kąt przy wierzchołku
kąt przy wierzchołku 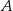 ma większą miarę, niż kąt przy wierzchołku
ma większą miarę, niż kąt przy wierzchołku 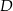 . Suma miar pewnych trzech kątów tego równoległoboku jest równa
. Suma miar pewnych trzech kątów tego równoległoboku jest równa 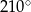 .
.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Miara kąta przy wierzchołku 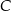 równoległoboku jest równa A/B .
równoległoboku jest równa A/B .
A) 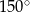 B)
B) 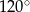
Miara kąta przy wierzchołku 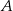 jest C/D razy większa od miary kąta przy wierzchołku
jest C/D razy większa od miary kąta przy wierzchołku 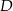 .
.
C) 4 D) 5
Do prostopadłościennego akwarium, o wymiarach podanych na rysunku, wlano 400 litrów wody.
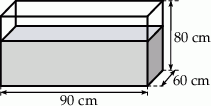
Czy włożenie do akwarium metalowego sześcianu o krawędzi 32 cm sprawi, że część wody się wyleje? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | objętość sześcianu jest mniejsza niż 40 litrów. |
| B) | objętość sześcianu jest większa niż 32 litry. |
| C) | długość krawędzi sześcianu jest mniejsza od długości każdej krawędzi akwarium. |
Cztery jednakowe drewniane elementy, każdy w kształcie prostopadłościanu o wymiarach 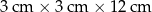 , przyklejono do metalowej płytki w sposób pokazany na rysunku I.
, przyklejono do metalowej płytki w sposób pokazany na rysunku I.
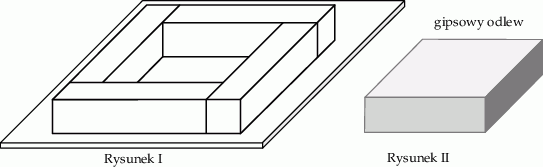
W ten sposób przygotowano formę, którą wypełniono masą gipsową, i tak otrzymano gipsowy odlew w kształcie prostopadłościanu, pokazany na rysunku II.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Objętość gipsowego odlewu jest równa C/D .
A) 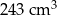 B)
B) 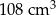
Objętość drewna, z którego zbudowano formę, jest równa A/B .
C) 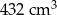 D)
D) 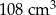
Na rysunku przedstawiono trójkąt 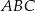 , w którym
, w którym 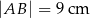 oraz odcinek
oraz odcinek 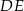 równoległy do boku
równoległy do boku 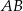 trójkąta, którego długość jest równa 6 cm.
trójkąta, którego długość jest równa 6 cm.
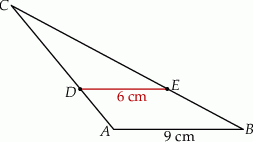
Pole trójkąta 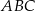 jest równe
jest równe 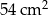 , a pole trapezu
, a pole trapezu 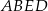 jest o 25% większe od pola trójkąta
jest o 25% większe od pola trójkąta 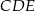 . Oblicz wysokość trapezu
. Oblicz wysokość trapezu 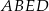 .
.
Cztery jednakowe prostopadłościenne klocki, każdy o wymiarach 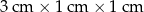 , ułożono tak, jak przedstawiono na rysunku.
, ułożono tak, jak przedstawiono na rysunku.
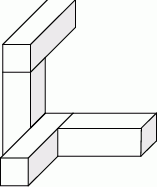
Następnie do tej budowli dołożono sześcienne klocki o krawędzi długości 1 cm tak, aby powstał prostopadłościan najmniejszy z możliwych. Ile sześciennych klocków o krawędzi długości 1 cm dołożono do tej budowli? Jakie są wymiary otrzymanego prostopadłościanu?
W pojemniku znajduje się 215 kolorowych plastikowych klocków o jednakowym kształcie. Wśród tych klocków jest 49 klocków czerwonych, 25 niebieskich, 39 żółtych. Pozostałe klocki są zielone. Kacper, nie zaglądając do pudełka, wyjmuje z niego kolejno po jednym klocku. Ile co najmniej klocków musi wyjąć Kacper, żeby mieć pewność, że wśród wyjętych klocków są co najmniej po dwa klocki w każdym z kolorów.
Prostokątny pasek papieru o wymiarach 26 cm na 2 cm jest z jednej strony biały, a z drugiej – szary. Ten pasek złożono w sposób pokazany na rysunku.
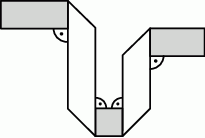
Pole widocznej szarej części paska jest równe 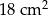 . Jakie pole ma widoczna biała część paska?
. Jakie pole ma widoczna biała część paska?
Na początku wakacji za zestaw złożony z płetw, okularów pływackich i kąpielówek trzeba było zapłacić 195 zł, przy czym cena samych płetw była równa 84 zł, a cena samych okularów pływackich była równa 56 zł. We wrześniu płetwy przeceniono o 15%, kąpielówki przeceniono o 20% i cały zestaw składający się z płetw, okularów pływackich i kąpielówek można było kupić za 149 zł. O ile procent przeceniono okulary pływackie?
Trzy pracujące jednocześnie pompy wypompowały 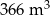 wody, przy czym wydajność pierwszej pompy była o 20% niższa niż wydajność trzeciej pompy, a wydajność drugiej pompy była o 20% niższa niż wydajność pierwszej pompy. Łączny koszt pracy pomp wyniósł 1464 zł, przy czym koszt pracy każdej z pomp był proporcjonalny do jej wydajności. Jaki był koszt pracy każdej z pomp?
wody, przy czym wydajność pierwszej pompy była o 20% niższa niż wydajność trzeciej pompy, a wydajność drugiej pompy była o 20% niższa niż wydajność pierwszej pompy. Łączny koszt pracy pomp wyniósł 1464 zł, przy czym koszt pracy każdej z pomp był proporcjonalny do jej wydajności. Jaki był koszt pracy każdej z pomp?

