Zestaw użytkownika nr 4954_7656
FunkcjeFunkcje kwadratowe
Wyznacz wzór funkcji 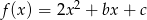 w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania
w postaci kanonicznej wiedząc, że jej miejsca zerowe są rozwiązaniami równania 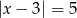 .
.
Jednym z miejsc zerowych funkcji kwadratowej 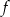 jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to
jest liczba 5, maksymalny przedział, w którym ta funkcja jest malejąca to 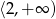 . Największa wartość funkcji
. Największa wartość funkcji 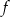 w przedziale
w przedziale 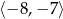 jest równa
jest równa 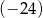 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 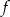 i narysuj jej wykres.
i narysuj jej wykres.
Wiesz, że funkcja kwadratowa 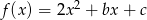 przyjmuje wartość najmniejszą
przyjmuje wartość najmniejszą 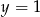 dla
dla 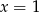 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 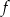 , a następnie rozwiąż równanie
, a następnie rozwiąż równanie 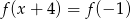 .
.
Zbiorem wartości funkcji kwadratowej 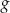 jest przedział
jest przedział 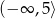 , a zbiorem rozwiązań nierówności
, a zbiorem rozwiązań nierówności 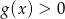 jest przedział
jest przedział 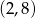 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 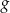 .
.
W poniższej tabeli podane są wartości funkcji kwadratowej 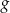 dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
dla kilku wybranych argumentów zapisanych w kolejności rosnącej:
| x | -2 | -1 | 0 | 1 | |
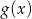 | -4 | 1 | 2 | -1 |
- Wyznacz wzór funkcji
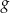 .
. - Uzupełnij brakujące zapisy w tabeli.
- Rozwiąż nierówność
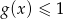 .
.
Funkcja kwadratowa określona wzorem 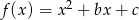 osiąga wartości ujemne wtedy i tylko wtedy, gdy
osiąga wartości ujemne wtedy i tylko wtedy, gdy 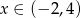 .
.
- Wyznacz wartości współczynników
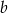 i
i  .
. - Oblicz, dla jakich argumentów
 , wartości funkcji
, wartości funkcji 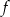 są mniejsze od wartości funkcji kwadratowej
są mniejsze od wartości funkcji kwadratowej 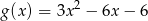 .
. - Rozwiąż równanie
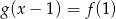 .
.
Wyznacz najmniejszą i największą wartość funkcji 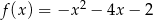 w przedziale
w przedziale 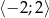 .
.
Dane są dwie funkcje kwadratowe 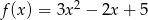 i
i 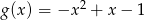 . Wyznacz największą wartość funkcji
. Wyznacz największą wartość funkcji 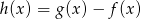 .
.
Określ zbiór wartości i przedziały monotoniczności funkcji 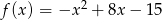 .
.
Dany jest trójmian kwadratowy 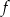 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 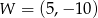 . Oblicz
. Oblicz 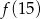 .
.

