Zestaw użytkownika nr 4965_2753

Zestaw użytkownika
nr 4965_2753

Zadanie 1

(4 pkt)

Dla jakich wartości parametru 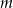równanie 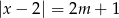|x − 2| = 2m + 1 ma jedno rozwiązanie?

Zadanie 2

(5 pkt)

Określ liczbę pierwiastków równania 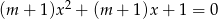2 (m + 1 )x + (m + 1)x + 1 = 0 w zależności od wartości parametru 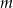, a następnie naszkicuj wykres funkcji:

( |{ x1 + x2 gdy dane równanie ma dwa pierwiastki x1 i x2, f(m ) = |( 2x0 gdy dane równanie ma jeden pierwiastek x 0, 3− m gdy dane równanie nie ma pierwiastków .

Zadanie 3

(5 pkt)

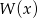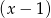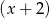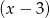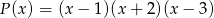Wielomian W (x) przy dzieleniu przez dwumiany (x − 1) , (x+ 2) , (x − 3) daje reszty odpowiednio równe 5, 2, 27. Wyznacz resztę z dzielenia tego wielomianu przez wielomian P (x) = (x − 1 )(x+ 2)(x− 3) .

Zadanie 4

(4 pkt)

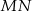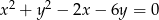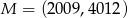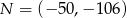Ile punktów wspólnych ma prosta z okręgiem 2 2 x + y − 2x − 6y = 0 jeśli M = (2009,40 12) oraz N = (− 50,− 106) .

Zadanie 5

(4 pkt)

Suma dwóch liczb jest równa 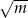√ -- m , a ich różnica jest równa 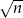√ -- n , gdzie 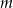i są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.

Zadanie 6

(5 pkt)

Rozwiąż równanie 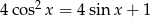2 4co s x = 4 sin x + 1 w przedziale ⟨0,2π ⟩ .

Zadanie 7

(4 pkt)

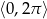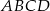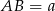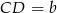Podstawy trapezu ABCD mają długości AB = a i CD = b . Na ramionach trapezu wybrano punkty 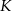i 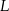w ten sposób, że odcinek 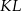jest równoległy do podstaw i przechodzi przez punkt przecięcia przekątnych. Oblicz długość odcinka .

Zadanie 8

(5 pkt)

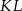Zaznacz w układzie współrzędnych zbiór wszystkich par 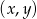(x,y) liczb rzeczywistych, dla których wyrażenie: 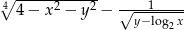∘ ------------ 4 4 − x2 − y2 − √---1---- y−log2x ma wartości rzeczywiste.

Zadanie 9

(4 pkt)

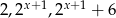Znajdź , dla którego liczby x+ 1 x+1 2,2 ,2 + 6 w podanej kolejności tworzą ciąg arytmetyczny.

Rozwiąż on-line Arkusz Wersja PDF