Zestaw użytkownika nr 5070_6619
Zestaw użytkownika
nr 5070_6619
Ciągiem geometrycznym jest ciąg określony wzorem
A) 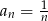 B)
B) 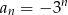 C)
C) 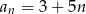 D)
D) 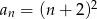
Trzeci wyraz ciągu geometrycznego jest równy 4, a czwarty wyraz tego ciągu jest równy -2. Pierwszy wyraz tego ciągu jest równy
A) -16 B) -8 C) 8 D) 16
W ciągu geometrycznym pierwszy wyraz 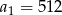 , a iloraz
, a iloraz 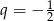 . Ósmy wyraz tego ciągu jest równy
. Ósmy wyraz tego ciągu jest równy
A) 4 B) 2 C) -2 D) -4
Dany jest ciąg arytmetyczny, w którym 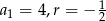 . Wtedy
. Wtedy
A) 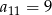 B)
B) 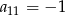 C)
C) 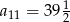 D)
D) 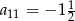
Dany jest ciąg o wyrazie ogólnym 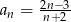 . Wynika stąd, że
. Wynika stąd, że
A) 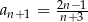 B)
B) 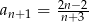 C)
C) 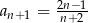 D)
D) 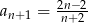
Iloczyn pierwszych 5 wyrazów ciągu geometrycznego danego wzorem 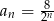 , gdzie
, gdzie 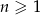 jest równy
jest równy
A) 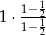 B)
B) 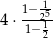 C)
C) 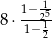 D)
D) 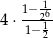
Ciąg 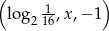 jest geometryczny. Wynika z tego, że
jest geometryczny. Wynika z tego, że
A) 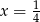 B)
B) 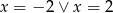 C)
C) 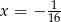 D)
D) 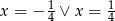
Suma trzydziestu początkowych wyrazów ciągu arytmetycznego 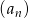 danego wzorem
danego wzorem 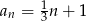 jest równa
jest równa
A) 11 B) 370 C) 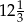 D) 185
D) 185
Dany jest ciąg arytmetyczny o pierwszym wyrazie 6 i różnicy 2. Wyraz ogólny ciągu wyraża się wzorem
A) 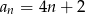 B)
B) 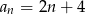 C)
C) 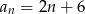 D)
D) 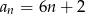
Suma trzech pierwszych wyrazów ciągu geometrycznego jest równa 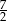 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy 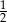 . Czwarty wyraz tego ciągu jest równy
. Czwarty wyraz tego ciągu jest równy
A) 0,25 B) -0,25 C) 1 D) -1
Dany jest ciąg geometryczny o wyrazie ogólnym 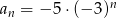 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy
A) 45 B) -135 C) -45 D) 135
Ciąg arytmetyczny 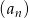 określony jest wzorem
określony jest wzorem 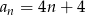 . Zatem suma
. Zatem suma 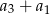 jest równa
jest równa
A) 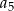 B)
B) 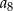 C)
C) 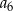 D)
D) 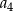
Suma 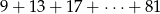 kolejnych wyrazów ciągu arytmetycznego jest równa
kolejnych wyrazów ciągu arytmetycznego jest równa
A) 851 B) 855 C) 1710 D) 859
W ciągu geometrycznym drugi wyraz jest równy 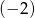 , a trzeci wyraz
, a trzeci wyraz 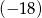 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) -9 B) -3 C) 3 D) 9
Ciąg 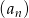 określony jest wzorem
określony jest wzorem 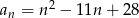 , gdzie
, gdzie 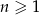 . Liczba niedodatnich wyrazów tego ciągu jest równa
. Liczba niedodatnich wyrazów tego ciągu jest równa
A) 3 B) 4 C) 7 D) 2
Liczby 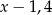 i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba
i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba  jest równa
jest równa
A) -7 B) -1 C) 1 D) 3
Pierwszy wyraz ciągu arytmetycznego jest równy 9, a różnica wynosi 7. Wyrazem tego ciągu jest liczba
A) 12 B) 19 C) 44 D) 54
Ciągiem rosnącym jest ciąg o wyrazie ogólnym
A) 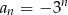 B)
B) 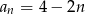 C)
C) 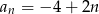 D)
D) 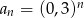
Trzeci wyraz ciągu geometrycznego jest równy 4, a piąty wyraz tego ciągu jest równy 1. Pierwszy wyraz tego ciągu jest równy
A) 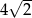 B)
B) 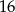 C) 4 D)
C) 4 D) 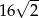
W ciągu geometrycznym 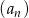 dane są
dane są 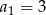 i
i 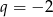 . Suma ośmiu początkowych wyrazów tego ciągu jest równa
. Suma ośmiu początkowych wyrazów tego ciągu jest równa
A) 255 B) 257 C) -257 D) -255
Trzy liczby tworzą ciąg geometryczny. Iloczyn tych liczb jest równy 216. Drugi wyraz tego ciągu jest równy
A) 36 B) 6 C) 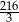 D) 12
D) 12
Ciąg arytmetyczny tworzą liczby
A) 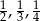 B) 2,4,8 C) -5,-3,-1 D)
B) 2,4,8 C) -5,-3,-1 D) 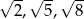
Piąty wyraz ciągu arytmetycznego jest równy 17, a różnica tego ciągu jest równa 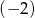 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 11 B) 25 C) 23 D) 9
Różnica ciągu arytmetycznego 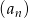 o wyrazie ogólnym
o wyrazie ogólnym 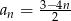 jest równa
jest równa
A) 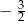 B) -2 C) 3 D) -3
B) -2 C) 3 D) -3
Ciąg 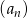 określony jest wzorem
określony jest wzorem 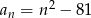 , gdzie
, gdzie 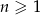 . Liczba ujemnych wyrazów tego ciągu jest równa
. Liczba ujemnych wyrazów tego ciągu jest równa
A) 10 B) 9 C) 8 D) 17
W ciągu geometrycznym 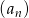 dane są:
dane są: 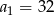 i
i 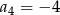 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 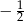 B) -12 C) 12 D)
B) -12 C) 12 D) 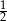
W ciągu arytmetycznym 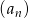 dane są:
dane są: 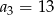 i
i 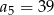 . Wtedy wyraz
. Wtedy wyraz 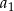 jest równy
jest równy
A) -26 B) 13 C) -13 D) 0
W ciągu arytmetycznym o różnicy 4 siódmy wyraz wynosi 33. Pierwszy wyraz tego ciągu jest równy
A) 9 B) 132 C) 5 D) 29
Który z podanych ciągów jest ciągiem geometrycznym?
A) 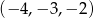 B)
B) 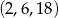 C)
C) 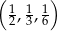 D)
D) 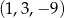
Ciąg 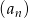 o wyrazie ogólnym
o wyrazie ogólnym 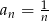 jest ciągiem
jest ciągiem
A) geometrycznym B) malejącym C) arytmetycznym D) rosnącym
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 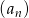 wyraża się wzorem
wyraża się wzorem 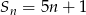 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz ciągu
-ty wyraz ciągu 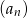 dla
dla 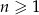 .
.
Dany jest ciąg 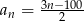 .
.
- Oblicz piętnasty wyraz tego ciągu.
- Którym wyrazem tego ciągu jest liczba 10.
- Ile wyrazów ujemnych ma ten ciąg?
Iloraz ciągu geometrycznego 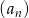 równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.
równy jest 3, a suma odwrotności wyrazu pierwszego i drugiego wynosi 18.
- Oblicz pierwszy wyraz ciągu
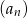 .
. - Podaj wzór na wyraz ogólny ciągu
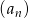 .
.
Nieskończony ciąg liczbowy 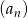 dla
dla 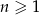 jest określony wzorem
jest określony wzorem
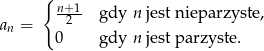
- Uzupełnij tabelkę:

1 2 3 4 5 
2005 2006 2007 2008 
1 0 … - Oblicz
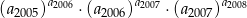 .
. - Oblicz sumę 2008 początkowych wyrazów ciągu
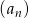 .
.
Ciąg 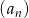 określony jest wzorem
określony jest wzorem 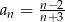 .
.
- Oblicz dziesiąty wyraz ciągu.
- Oblicz, który wyraz ciągu jest równy
 .
.
Pan Kowalski planując wyjazd na wakacje letnie w następnym roku postanowił założyć lokatę, wpłacając do banku 2000 zł na okres jednego roku. Ma do wyboru trzy rodzaje lokat: lokata 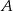 – oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;
– oprocentowanie w stosunku rocznym 5%, kapitalizacja odsetek po roku;
lokata 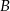 – oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;
– oprocentowanie w stosunku rocznym 4,8%, kapitalizacja odsetek co pół roku;
lokata 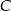 – oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
– oprocentowanie w stosunku rocznym 4,6%, kapitalizacja odsetek co kwartał.
Oceń, wykonując odpowiednie obliczenia, która lokata jest najkorzystniejsza dla Pana Kowalskiego.
Pan Kwiatkowski i pan Kowalski wpłacili swoje oszczędności o łącznej wartości 10 000 zł do różnych banków. Pan Kwiatkowski ulokował swoje oszczędności w banku, w którym oprocentowanie rocznie wynosiło 12% zaś pan Kowalski - w banku, który proponował oprocentowanie roczne w wysokości 14%. Po roku łączna kwota odsetek wynosiła 1384 zł. Ile złotych ulokował w banku każdy z panów?
Sprawdź, czy liczby 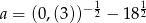 ,
, 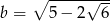 ,
, 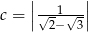 są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
są w podanej kolejności kolejnymi wyrazami ciągu arytmetycznego.
Czwarty wyraz ciągu arytmetycznego jest równy 6. Oblicz sumę siedmiu początkowych wyrazów tego ciągu.
Iloraz ciągu geometrycznego 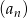 jest równy
jest równy 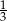 , a suma jego pięciu początkowych wyrazów wynosi -605. Znajdź pierwszy wyraz ciągu
, a suma jego pięciu początkowych wyrazów wynosi -605. Znajdź pierwszy wyraz ciągu 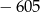 oraz określ jego monotoniczność.
oraz określ jego monotoniczność.

