Zestaw użytkownika nr 5098_4851
Planimetria 2
W rombie jedna z przekątnych jest dłuższa od drugiej o 3 cm. Dla jakich długości przekątnych pole rombu jest większe od 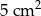 ?
?
Czy istnieje taki wielokąt, który ma 2 razy więcej przekątnych niż boków?
Do dwóch okręgów o promieniach długości 3cm i 10cm poprowadzono wspólną styczną tak, że okręgi znajdują się po różnych stronach tej stycznej. Odległość między środkami okręgów wynosi 39 cm. Oblicz długość odcinka między punktami styczności.
Wyznacz promień okręgu wpisanego w trójkąt równoramienny o ramieniu długości 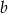 i kącie o mierze
i kącie o mierze  przy podstawie.
przy podstawie.
Na bokach 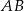 i
i 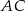 trójkąta
trójkąta 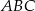 , który nie jest równoramienny, wybrano takie punkty
, który nie jest równoramienny, wybrano takie punkty 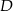 i
i 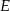 , że
, że 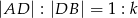 oraz
oraz 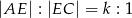 , dla
, dla 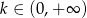 .
.
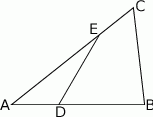
- Wyznacz wzór funkcji
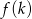 , która jest zdefiniowana jako stosunek pól trójkątów
, która jest zdefiniowana jako stosunek pól trójkątów 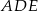 i
i 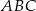 .
. - Wiedząc że
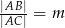 , dla
, dla 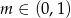 wyznacz wszystkie wartości parametru
wyznacz wszystkie wartości parametru 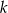 , dla których trójkąty
, dla których trójkąty 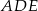 i
i 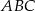 są podobne.
są podobne.
Pole trapezu jest równe 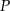 , a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
, a stosunek długości podstaw trapezu wynosi 2. Przekątne dzielą ten trapez na cztery trójkąty. Oblicz pole każdego z tych trójkątów.
Suma długości dwóch boków trójkąta wynosi 6 cm, a miara kąta pomiędzy tymi bokami wynosi 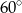 . Jaką najmniejszą wartość ma obwód tego trójkąta.
. Jaką najmniejszą wartość ma obwód tego trójkąta.
Rysunek przedstawia kształt obszaru zakreślanego przez wycieraczkę samochodową.
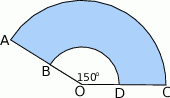
Wiedząc, że 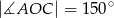 oraz
oraz 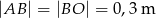 oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że
oblicz jakie jest pole obszaru oczyszczanego przez wycieraczkę. Przyjmując, że 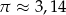 podaj wynik z dokładnością do
podaj wynik z dokładnością do 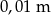 .
.
W trapezie równoramiennym, który nie jest równoległobokiem, ramię ma długość 7 cm, a przekątna 8 cm. Oblicz długości podstaw trapezu wiedząc, że odcinek łączący środki ramion trapezu ma długość 4 cm.
W trapezie równoramiennym długość krótszej podstawy wynosi 9 cm, przekątnej 17 cm a ramienia 10 cm. Oblicz jego pole.
Punkt 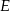 leży na ramieniu
leży na ramieniu 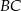 trapezu
trapezu 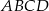 , w którym
, w którym 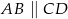 . Udowodnij, że
. Udowodnij, że 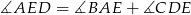 .
.
Dane jest koło o promieniu długości 16 cm. W kole tym poprowadzono cięciwę opartą na łuku odpowiadającym kątowi środkowemu o mierze 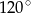 . Znajdź odległość tej cięciwy od środka koła.
. Znajdź odległość tej cięciwy od środka koła.
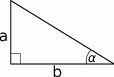
Dany jest trójkąt prostokątny, w którym  ,
, 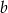 oznaczają długości przyprostokątnych,
oznaczają długości przyprostokątnych,  jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej
jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej  . Wiadomo, że
. Wiadomo, że 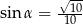 . Oblicz
. Oblicz
- tangens kąta
 ;
; - wartość wyrażenia
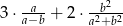 .
.
Podaj wymiary prostokąta, którego boki różnią się o 6 cm, a przekątna ma długość 30 cm.
Dany jest równoramienny trójkąt prostokątny, którego przeciwprostokątna ma długość 2. Bok 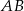 prostokąta
prostokąta 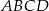 zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty
zawiera się w przeciwprostokątnej tego trójkąta, zaś punkty 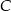 i
i 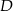 należą do przyprostokątnych. Oblicz długości boków prostokąta
należą do przyprostokątnych. Oblicz długości boków prostokąta 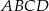 wiedząc, że kwadrat długości jego przekątnej
wiedząc, że kwadrat długości jego przekątnej 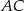 ma wartość najmniejszą z możliwych.
ma wartość najmniejszą z możliwych.
Liczby 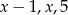 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Z punktu 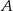 leżącego na okręgu o promieniu
leżącego na okręgu o promieniu 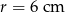 i środku
i środku 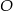 poprowadzono dwie równej długości cięciwy
poprowadzono dwie równej długości cięciwy 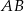 i
i 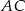 tworzące kąt
tworzące kąt 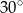 . Oblicz pole czworokąta
. Oblicz pole czworokąta 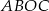 .
.
W prostokącie połączono środki sąsiednich boków. Powstały w ten sposób romb ma obwód 40 cm i pole równe 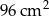 . Oblicz długości boków prostokąta.
. Oblicz długości boków prostokąta.
Przyprostokątne trójkąta prostokątnego 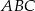 mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek
mają długości 12 i 6. Oblicz długość promienia okręgu stycznego do obu przyprostokątnych, którego środek 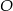 leży na przeciwprostokątnej, oraz oblicz odległości środka
leży na przeciwprostokątnej, oraz oblicz odległości środka 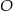 od wierzchołków trójkąta
od wierzchołków trójkąta 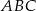 .
.
Jaki warunek musi spełniać liczba  , aby istniał trójkąt o bokach
, aby istniał trójkąt o bokach 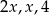 ?
?
Dany jest trójkąt równoboczny 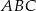 . Okrąg o średnicy
. Okrąg o średnicy 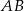 przecina bok
przecina bok 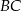 w punkcie
w punkcie 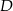 .
.
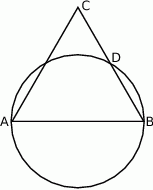
Wykaż, że 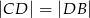 .
.
Punkt 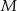 jest punktem wspólnym przekątnych trapezu prostokątnego
jest punktem wspólnym przekątnych trapezu prostokątnego 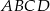 . Punkt
. Punkt 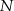 jest punktem wspólnym przekątnej
jest punktem wspólnym przekątnej 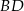 i wysokości
i wysokości 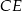 opuszczonej na dłuższą podstawę
opuszczonej na dłuższą podstawę 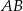 . Wykaż, że
. Wykaż, że 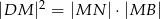 .
.
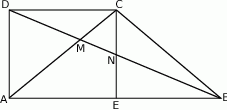
Udowodnij, że trzy środkowe rozcinają trójkąt na sześć części o równych polach.
Dany jest trójkąt prostokątny o polu 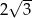 i kącie ostrym
i kącie ostrym 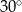 . Oblicz długości przyprostokątnych tego trójkąta.
. Oblicz długości przyprostokątnych tego trójkąta.
Liczba przekątnych wielokąta wypukłego, w którym jest  boków i
boków i 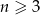 wyraża się wzorem
wyraża się wzorem 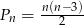 .
.
- Oblicz liczbę przekątnych w dwudziestokącie wypukłym.
- Oblicz, ile boków ma wielokąt wypukły, w którym liczba przekątnych jest pięć razy większa od liczby boków.
- Sprawdź, czy jest prawdziwe następujące stwierdzenie: Każdy wielokąt wypukły o parzystej liczbie boków ma parzystą liczbę przekątnych. Odpowiedź uzasadnij.
- Uzasadnij, że jeżeli liczba boków wielokąta wypukłego jest nieparzysta, to liczba jego przekątnych jest wielokrotnością liczby jego boków.
Kąt ostry między przekątnymi równoległoboku 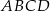 ma miarę
ma miarę 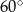 . Przekątna
. Przekątna 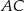 ma długość 6, a przekątna
ma długość 6, a przekątna 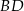 jest prostopadła do boku
jest prostopadła do boku 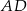 . Oblicz długości boków równoległoboku.
. Oblicz długości boków równoległoboku.
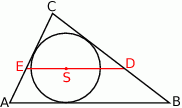
Przez środek 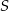 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 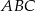 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 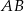 , która przecina boki
, która przecina boki 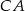 i
i 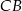 odpowiednio w punktach
odpowiednio w punktach 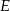 i
i 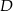 .
.
Wykaż, że 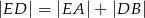 .
.
Na bokach 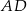 i
i 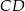 kwadratu
kwadratu 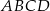 o boku długości 1 wybrano punkty
o boku długości 1 wybrano punkty 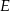 i
i 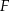 w ten sposób, że
w ten sposób, że 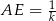 i
i 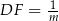 , dla
, dla 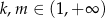 . Niech
. Niech 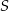 będzie punktem przecięcia odcinków
będzie punktem przecięcia odcinków 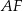 i
i 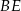
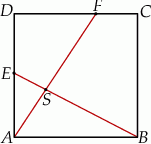
- Wykaż, że jeżeli trójkąt
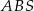 jest prostokątny to
jest prostokątny to 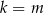 .
. - Oblicz cosinus kąta
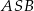 jeżeli
jeżeli 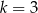 i
i 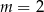 .
.
Krótsza przekątna rombu o długości 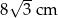 dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
dzieli go na dwa trójkąty równoboczne. Oblicz pole rombu.
Dany jest trapez prostokątny 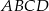 o podstawach
o podstawach 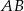 i
i 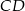 , w którym boki
, w którym boki 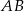 i
i 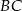 są prostopadłe. Dwusieczne kątów
są prostopadłe. Dwusieczne kątów 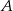 i
i 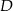 przecinają się w punkcie
przecinają się w punkcie 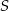 leżącym na boku
leżącym na boku 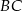 . Wykaż, że
. Wykaż, że 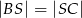 .
.
W okręgu o promieniu 5 poprowadzono dwie równoległe cięciwy o długościach 6 i 8. Oblicz odległość między tymi cięciwami.
Dany jest pięciokąt foremny 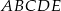 o boku długości
o boku długości  . Wiedząc, że
. Wiedząc, że 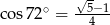
- wykaż, że długość przekątnej pięciokąta
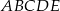 jest równa
jest równa 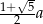 ;
; - oblicz długość promienia okręgu wpisanego w pięciokąt
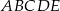 .
.
Dany jest trójkąt o wymiarach 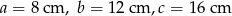 . Oblicz obwód trójkąta podobnego w skali 5.
. Oblicz obwód trójkąta podobnego w skali 5.
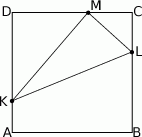
Na bokach 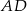 ,
, 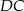 i
i 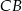 kwadratu
kwadratu 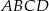 wybrano punkty
wybrano punkty 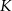 ,
, 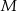 i
i 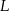 ten sposób, że
ten sposób, że 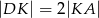 ,
, 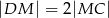 , oraz
, oraz 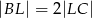 .
.
- Uzasadnij, że trójkąt
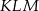 jest prostokątny.
jest prostokątny. - Oblicz tangensy kątów ostrych trójkąta
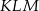 .
.
Pole rombu jest równe 120. Gdyby zwiększyć długości jego przekątnych odpowiednio o 2 i 5 to pole wzrosłoby o 55. Oblicz obwód rombu. Podaj wszystkie możliwe odpowiedzi.
W trójkącie równobocznym 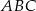 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt 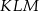 . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów 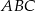 i
i 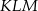 .
.
Liczby 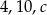 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
Dany jest czworokąt wypukły 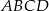 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 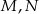 są odpowiednio środkami boków
są odpowiednio środkami boków 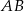 i
i 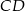 . Punkty
. Punkty 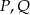 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 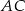 i
i 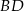 . Uzasadnij, że
. Uzasadnij, że 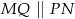 .
.
W prostokącie 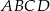 , w którym stosunek długości boków
, w którym stosunek długości boków 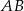 i
i 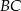 jest równy 4:3, poprowadzono dwusieczne kątów
jest równy 4:3, poprowadzono dwusieczne kątów 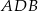 i
i 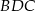 . Dwusieczne te przecinają boki
. Dwusieczne te przecinają boki 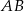 i
i 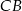 odpowiednio w punktach
odpowiednio w punktach 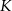 i
i 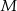 . Oblicz stosunek pola prostokąta
. Oblicz stosunek pola prostokąta 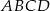 do pola trójkąta
do pola trójkąta 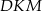 .
.
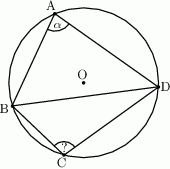
Wszystkie wierzchołki czworokąta 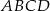 leżą na okręgu oraz
leżą na okręgu oraz 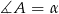 . Oblicz miarę kąta
. Oblicz miarę kąta 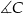 .
.