Zestaw użytkownika nr 5119_1671
Zestaw użytkownika
nr 5119_1671
Z urny, w której jest 6 kul czarnych i 4 żółte, wyjęto dwa razy po jednej kuli ze zwracaniem. Oblicz prawdopodobieństwo, że wyjęto kule jednakowych kolorów.
Dane są zbiory liczb całkowitych: 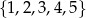 i
i 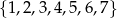 . Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
. Z każdego z tych zbiorów wybieramy losowo po jednej liczbie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb będzie podzielna przez 5.
Spośród 5 monet jednozłotowych, 7 dwuzłotowych i 6 pięciozłotowych wybieramy 3 monety. Oblicz prawdopodobieństwo, że wszystkie trzy monety będą miały ten sam nominał.
O zdarzeniach losowych 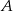 i
i 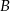 wiemy, że:
wiemy, że: 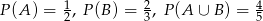 . Oblicz:
. Oblicz:
W wazonie stoi 12 czerwonych i 8 żółtych róż. Pani Krystyna wyjęła losowo dwie róże z wazonu. Oblicz prawdopodobieństwo, że wśród wybranych kwiatów jest przynajmniej jedna róża żółta.
10 kul rozmieszczamy w 10 szufladach. Jakie jest prawdopodobieństwo tego, że każda szuflada będzie zajęta?
Dla zdarzeń 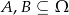 spełnione są warunki
spełnione są warunki 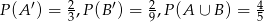 . Oblicz
. Oblicz 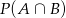 .
.
Wiadomo, że 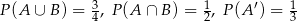 . Oblicz prawdopodobieństwa zdarzeń
. Oblicz prawdopodobieństwa zdarzeń 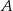 i
i 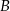 .
.
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 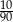 B)
B) 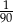 C)
C) 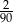 D)
D) 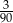
Jeżeli 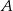 i
i 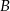 są zdarzeniami losowymi,
są zdarzeniami losowymi, 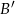 jest zdarzeniem przeciwnym do
jest zdarzeniem przeciwnym do 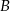 ,
, 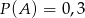 ,
, 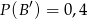 oraz
oraz 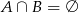 , to
, to 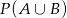 jest równe
jest równe
A) 0,12 B) 0,18 C) 0,9 D) 0,6
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania sumy oczek równej trzy wynosi
A) 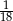 B)
B) 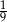 C)
C) 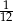 D)
D)