/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2023/Próbne testy
Próbny Egzamin Ósmoklasisty
z Matematyki Zestaw przygotowany przez serwis zadania.info 22 kwietnia 2023 Czas pracy: 100 minut
Na diagramie przedstawiono wyniki ankiety, w której działkowcy odpowiadali na pytanie „Jakiego ptaka najczęściej widują na swojej działce?”. Każdy ankietowany działkowiec podawał tylko jeden gatunek ptaka. Sikorkę wskazało 9 działkowców.
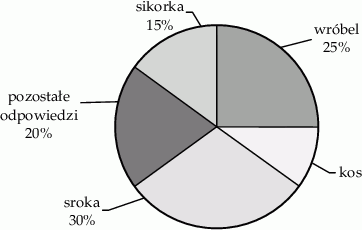
Które z podanych zdań jest fałszywe?
A) Sikorkę wskazało 2 razy mniej działkowców niż srokę.
B) Kosa wskazało 10% ankietowanych działkowców.
C) Kosa wskazało 6 ankietowanych działkowców.
D) W ankiecie wzięło udział 80 działkowców.
Wartość wyrażenia 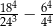 jest równa
jest równa
A) 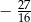 B)
B) 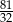 C)
C) 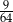 D)
D) 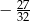
Dane są liczby: 12195, 43176, 54145, 57492, 61020, 37170.
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wśród danych liczb są dokładnie A/B liczby podzielne przez 12.
A) trzy B) cztery
Wśród danych liczb są dokładnie C/D liczby podzielne przez 45.
C) dwie D) trzy
Dane jest wyrażenie 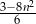 oraz liczby:
oraz liczby: 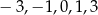 . Dla której z danych liczb wartość podanego wyrażenia jest największa?
. Dla której z danych liczb wartość podanego wyrażenia jest największa?
A) 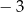 B)
B) 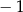 C) 0 D) 1 E) 3
C) 0 D) 1 E) 3
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 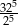 jest równa A/B .
jest równa A/B .
A) 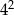 B)
B) 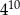
Wartość wyrażenia 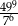 jest równa C/D .
jest równa C/D .
C) 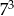 D)
D) 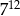
Suma siedemdziesięciu czterech liczb dodatnich jest równa 1978. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Po zmniejszeniu każdej z tych liczb o 6 suma otrzymanych liczb będzie równa 1536. | P | F |
| Po zwiększeniu każdej z tych liczb o 50% suma otrzymanych liczb będzie równa 2967. | P | F |
Pudełko margaryny o masie 40 dag przed promocją kosztowało 6,60 zł. Producent margaryny przygotował dwie promocje.

Czy dla klienta kupującego 440 dag margaryny bardziej opłacalna jest promocja II niż I? Wybierz odpowiedź T albo N i jej uzasadnienie spośród A, B albo C.
| Tak | Nie |
| ponieważ | |
| A) | w promocji I 1 dag margaryny kosztuje mniej niż w promocji II. |
| B) | w promocji II masa pudełka margaryny wzrośnie o 4 dag, natomiast w promocji I masa się nie zmieni. |
| C) | w promocji I trzeba kupić 11 pudełek margaryny, natomiast w promocji II – tylko 10. |
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Liczba 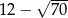 jest A/B .
jest A/B .
A) większa od 3 i mniejsza od 4. B) większa od 4 i mniejsza od 5.
Liczba 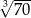 jest C/D .
jest C/D .
C) większa od 3 i mniejsza od 4. D) większa od 4 i mniejsza od 5.
Na osi liczbowej zaznaczono punkty 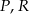 i
i 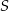 oraz podano współrzędne punktów
oraz podano współrzędne punktów 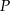 i
i 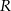 . Odcinek
. Odcinek 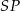 jest podzielony na 8 równych części (zobacz rysunek poniżej).
jest podzielony na 8 równych części (zobacz rysunek poniżej).
![]()
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Współrzędna punktu 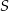 jest równa
jest równa
A) 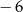 B)
B) 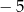 C)
C) 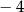 D)
D) 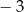
Pani Ewelina ma na działce trzy pojemniki: pojemnik zielony, którego objętość jest 1,5 razy mniejsza niż objętość pojemnika czerwonego, pojemnik czerwony o objętości 30 litrów oraz pojemnik niebieski o objętości 2,5 razy większej niż objętość pojemnika zielonego. Objętość pojemnika niebieskiego jest większa od objętości pojemnika czerwonego o
A) 30 litrów B) 20 litrów C) 10 litrów D) 15 litrów
Jacek otrzymał kieszonkowe, które w całości wydał w ciągu czterech kolejnych tygodni. W pierwszym tygodniu wydał  całej kwoty, w drugim tygodniu
całej kwoty, w drugim tygodniu 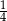 pozostałej kwoty, w trzecim tygodniu wydał dwa razy więcej pieniędzy niż w drugim tygodniu. W czwartym tygodniu wydał pozostałe 75 zł. Jeżeli przez
pozostałej kwoty, w trzecim tygodniu wydał dwa razy więcej pieniędzy niż w drugim tygodniu. W czwartym tygodniu wydał pozostałe 75 zł. Jeżeli przez  oznaczymy kwotę kieszonkowego, którą otrzymał Jacek, to sytuację przedstawioną w zadaniu opisuje równanie
oznaczymy kwotę kieszonkowego, którą otrzymał Jacek, to sytuację przedstawioną w zadaniu opisuje równanie
A) 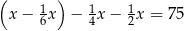
B) 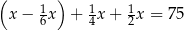
C) 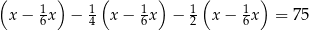
D) 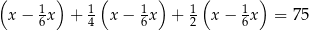
W pudełku znajdowały się piłeczki białe i czarne. Wśród wszystkich piłeczek 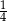 stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Kamil – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kamila piłeczki czarnej wynosi
stanowiły piłeczki czarne. Wyciągnięto 12 piłeczek, wśród których żadna nie była czarna. Kamil – jako trzynasty – losuje jedną piłeczkę. Prawdopodobieństwo wylosowania przez Kamila piłeczki czarnej wynosi 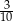 . Liczba wszystkich piłeczek czarnych, które początkowo znajdowały się w pudełku jest równa
. Liczba wszystkich piłeczek czarnych, które początkowo znajdowały się w pudełku jest równa
A) 18 B) 36 C) 24 D) 30
W trójkącie 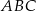 o obwodzie 128 cm poprowadzono odcinek
o obwodzie 128 cm poprowadzono odcinek 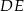 . Obwód trójkąta
. Obwód trójkąta 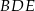 jest równy 84 cm, a obwód czworokąta
jest równy 84 cm, a obwód czworokąta 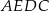 – 100 cm.
– 100 cm.
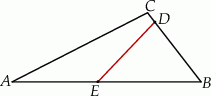
Długość odcinka 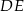 jest równa
jest równa
A) 56 cm B) 22 cm C) 14 cm D) 28 cm
Na rysunku przedstawiono siatkę graniastosłupa prostego, którego podstawą jest trapez. Na rysunku podano też długości niektórych jego krawędzi.
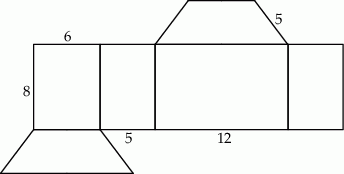
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Pole jednej ze ścian bocznych graniastosłupa jest dwa razy większe od pola jego podstawy. | P | F |
| Objętość tego graniastosłupa jest równa 288. | P | F |
Na rysunku przedstawiono trapez 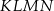 zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
zbudowany z trzech jednakowych trójkątów prostokątnych o przyprostokątnych długości 3 cm i 4 cm.
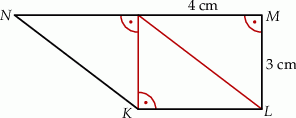
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Pole trapezu 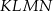 jest równe jest równe 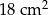 . . | P | F |
Obwód trapezu 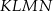 jest równy 18 cm. jest równy 18 cm. | P | F |
Do wykonania wyszywanego dekoltu z guzikami użyto 7 guzików perłowych, 8 guzików srebrnych i kilku guzików złotych. Złote guziki stanowią 25% wszystkich guzików w gotowym dekolcie. Oblicz, ile złotych guzików jest w gotowym dekolcie.
Kierowca o godz. 8:15 wyruszył w podróż z miejscowości Kulki do miejscowości Baryłki. Po drodze, o godz. 9:05 minął miejscowość Snopki, która znajduje się w odległości 60 km od miejscowości Baryłki. Do Baryłek kierowca dotarł o godz. 10:45 i okazało się, że całą trasę z Kulek do Baryłek pokonał ze średnią prędkością 40 km/h. Oblicz średnią prędkość, z jaką ten kierowca przejechał trasę z Kulek do Snopków. Wynik wyraź w 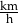 .
.
Na zawody sportowe miała pojechać grupa uczniów, w której miało być trzy razy więcej chłopców niż dziewcząt. Z powodu choroby na zawody nie pojechało dwóch chłopców i jedna dziewczynka. W konsekwencji, wśród uczniów, którzy pojechali na zawody liczba chłopców była równa 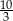 liczby dziewczynek. Ilu uczniów miało początkowo pojechać na te zawody?
liczby dziewczynek. Ilu uczniów miało początkowo pojechać na te zawody?
W prostokącie 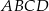 bok
bok 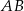 jest cztery razy dłuższy od boku
jest cztery razy dłuższy od boku 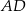 . Punkty
. Punkty 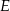 i
i 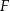 dzielą odcinek
dzielą odcinek 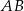 na trzy równe części (zobacz rysunek).
na trzy równe części (zobacz rysunek).

Oblicz pole trapezu 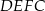 jeżeli wiadomo, że jego obwód jest równy 52 cm.
jeżeli wiadomo, że jego obwód jest równy 52 cm.

