Zestaw użytkownika nr 5139_3259
Zestaw użytkownika
nr 5139_3259
Zadanie 1
Wyznacz najmniejszą i największą wartość funkcji 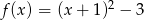 w przedziale
w przedziale 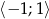 .
.
Zadanie 2
Dany jest trójmian kwadratowy 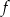 o współczynniku 2 przy najwyższej potędze
o współczynniku 2 przy najwyższej potędze  . Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne
. Wierzchołek paraboli będącej wykresem tego trójmianu ma współrzędne 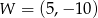 . Oblicz
. Oblicz 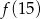 .
.
Zadanie 3
Znajdź taką wartość parametru 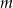 , aby największa wartość funkcji
, aby największa wartość funkcji 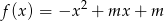 była najmniejsza z możliwych.
była najmniejsza z możliwych.
Zadanie 4
Dla jakich wartości parametru 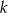 dziedziną funkcji
dziedziną funkcji 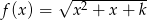 jest zbiór liczb rzeczywistych?
jest zbiór liczb rzeczywistych?
Zadanie 5
Do wykresu funkcji kwadratowej 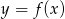 należą punkty
należą punkty 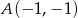 oraz
oraz 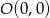 , który jest wierzchołkiem paraboli.
, który jest wierzchołkiem paraboli.
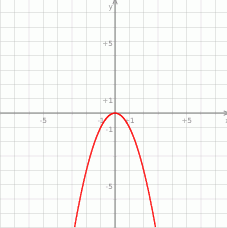
Wykres ten przesunięto w taki sposób, że otrzymano wykres funkcji 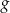 , której miejscami zerowymi są liczby 3 i 7.
, której miejscami zerowymi są liczby 3 i 7.
- Oblicz współrzędne wierzchołka paraboli będącej wykresem funkcji
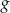 .
. - Narysuj wykres funkcji
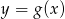 .
. - Rozwiąż nierówność
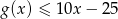 .
.

