Zestaw użytkownika nr 5198_2136
Zestaw użytkownika
nr 5198_2136
Liczba 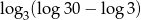 jest równa liczbie
jest równa liczbie
A) 1 B) 2 C) 0 D) -1
Wykaż, że liczba 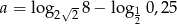 jest liczbą wymierną.
jest liczbą wymierną.
Liczba 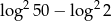 jest równa
jest równa
A) 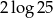 B)
B) 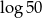 C)
C) 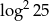 D)
D) 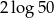
Liczba 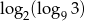 jest równa
jest równa
A) 2 B) -1 C) 1 D) -2
Oblicz 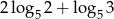 .
.
Jeśli 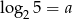 oraz
oraz 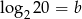 , to liczba
, to liczba 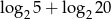 jest równa
jest równa
A) 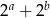 B)
B) 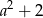 C)
C) 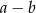 D)
D) 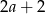
Liczba 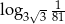 jest równa
jest równa
A) -6 B) 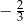 C)
C) 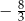 D) -8
D) -8
Wiadomo, że 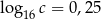 . Zatem liczba
. Zatem liczba  jest
jest
A) niewymierna B) wymierna C) większa od 2 D) mniejsza od 1
Jeżeli 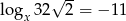 to liczba
to liczba  jest równa
jest równa
A) 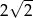 B)
B) 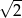 C)
C) 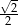 D) 2
D) 2
Oblicz wartość wyrażenia 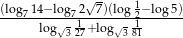 .
.
Wiedząc, że 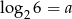 , wyznacz
, wyznacz 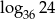 .
.
Oblicz 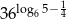 .
.
Liczba 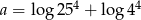 . Wynika stąd, że
. Wynika stąd, że
A) 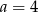 B)
B) 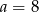 C)
C) 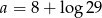 D)
D) 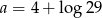
Wiadomo, że 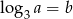 . Wtedy
. Wtedy 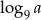 równa się
równa się
A) 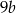 B)
B) 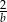 C)
C) 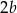 D)
D) 
Wartość wyrażenia 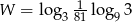 jest równa
jest równa
A) -3,5 B) -8 C) -3 D) -2
Liczba 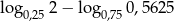 jest równa
jest równa
A) 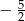 B) 0 C) 4 D)
B) 0 C) 4 D) 
O liczbie  wiadomo, że
wiadomo, że 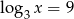 . Zatem
. Zatem
A) 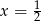 B)
B) 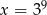 C)
C) 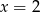 D)
D) 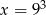
Liczba 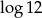 jest równa
jest równa
A) 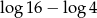 B)
B) 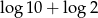 C)
C) 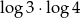 D)
D) 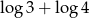
Liczba 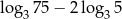 jest równa
jest równa
A) 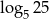 B)
B) 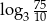 C)
C) 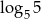 D)
D) 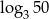
Liczba 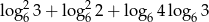 jest
jest
A) ujemna B) niewymierna C) mniejsza od 1 D) dodatnia
Liczba 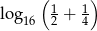 jest równa
jest równa
A) 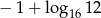 B) 6 C)
B) 6 C) 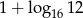 D) -6
D) -6
Nie korzystając z kalkulatora uzasadnij, że: 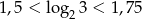 .
.
Liczba 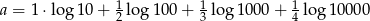 jest równa
jest równa
A) 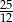 B) 11110 C) 4 D)
B) 11110 C) 4 D) 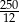
Liczba 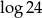 jest równa
jest równa
A) 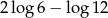 B)
B) 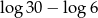 C)
C) 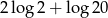 D)
D) 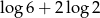
Nie używając kalkulatora, porównaj liczby: 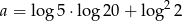 oraz
oraz 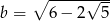 .
.
Jeżeli 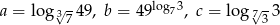 to
to
A) 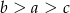 B)
B) 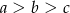 C)
C) 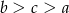 D)
D) 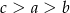
Udowodnij, że jeśli liczby dodatnie  i
i 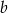 spełniają warunek
spełniają warunek 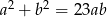 , to
, to 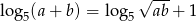 .
.
Oblicz 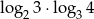 .
.
Która z liczb jest równa 2?
A) 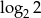 B)
B) 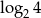 C)
C) 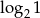 D)
D) 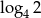
Która liczba nie jest liczbą całkowitą?
A) 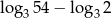 B)
B) 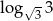 C)
C) 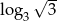 D)
D) 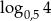
Wiadomo, że 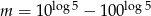 i
i 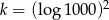 . Zatem
. Zatem
A) 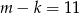 B)
B) 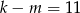 C)
C) 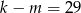 D)
D) 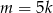
Wiedząc, że 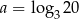 i
i 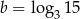 oblicz
oblicz 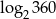 .
.

