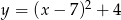Zestaw użytkownika nr 5233_2707
Sprawdzian Przekształcenia wykresów funkcji gr ASuma punktów: 15
Przesuwając wykres funkcji 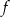 wzdłuż osi
wzdłuż osi  o 6 jednostek w prawo, otrzymano wykres funkcji
o 6 jednostek w prawo, otrzymano wykres funkcji  . Zatem
. Zatem
A) 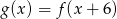 B)
B) 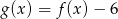 C)
C) 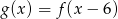 D)
D) 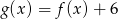
Aby na podstawie wykresu funkcji 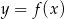 narysować wykres funkcji
narysować wykres funkcji 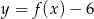 , należy wykres funkcji
, należy wykres funkcji  przesunąć o
przesunąć o
A) 6 jednostek do dołu
B) 6 jednostek w prawo
C) 6 jednostek do góry
D) 6 jednostek w lewo
Na rysunku przedstawiony jest wykres pewnej funkcji 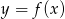 .
.
Naszkicuj na oddzielnych rysunkach wykresy funkcji: 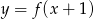 i
i 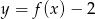 .
.
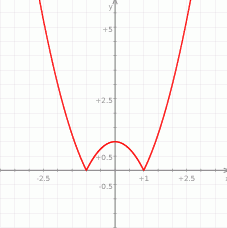
Dany jest wykres funkcji 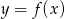 określonej dla
określonej dla 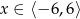 .
.
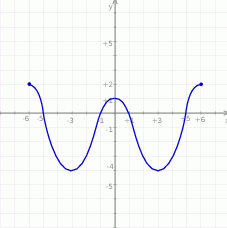
Korzystając z wykresu funkcji zapisz:
- maksymalne przedziały, w których funkcja jest rosnąca;
- zbiór argumentów, dla których funkcja przyjmuje wartości dodatnie;
- największą wartość funkcji
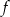 w przedziale
w przedziale 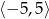 ;
; - miejsca zerowe funkcji
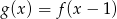 ;
; - najmniejszą wartość funkcji
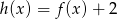 .
.
Wykres funkcji 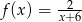 powstaje przez przesunięcie wykresu funkcji
powstaje przez przesunięcie wykresu funkcji 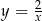 o 6 jednostek
o 6 jednostek
A) w lewo B) w prawo C) w górę D) w dół
Przesuwając wykres funkcji 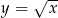 o dwie jednostki w górę otrzymujemy funkcję:
o dwie jednostki w górę otrzymujemy funkcję:
A) 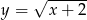 B)
B) 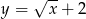 C)
C) 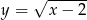 D)
D) 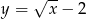
Dana jest funkcja 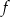 określona wzorem
określona wzorem 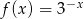 . Wykres funkcji
. Wykres funkcji 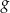 jest symetryczny do wykresu funkcji
jest symetryczny do wykresu funkcji 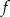 względem osi
względem osi 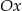 . Zatem
. Zatem
A) 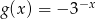 B)
B) 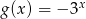 C)
C) 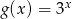 D)
D) 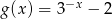
Gdy przesuniemy wykres funkcji 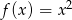 o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
o 7 jednostek w lewo i 4 jednostki w dół, to otrzymamy wykres funkcji
A) 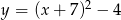 B)
B) 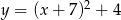 C)
C) 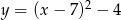 D)
D)