Zestaw użytkownika nr 5239_8195
Zestaw użytkownika
nr 5239_8195
Prosta równoległa do jednego boku trójkąta dzieli jego pole na połowy. W jakim stosunku prosta ta dzieli pozostałe boki trójkąta?
Przyprostokątne trójkąta 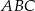 mają długości 10 i 24. Przeciwprostokątna trójkąta
mają długości 10 i 24. Przeciwprostokątna trójkąta 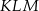 podobnego do niego ma długość 39. Oblicz pole trójkąta
podobnego do niego ma długość 39. Oblicz pole trójkąta 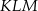 .
.
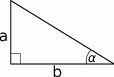
Dany jest trójkąt prostokątny, w którym  ,
, 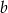 oznaczają długości przyprostokątnych,
oznaczają długości przyprostokątnych,  jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej
jest miarą kąta ostrego leżącego naprzeciw przyprostokątnej  . Wiadomo, że
. Wiadomo, że 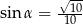 . Oblicz
. Oblicz
- tangens kąta
 ;
; - wartość wyrażenia
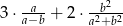 .
.
Liczby 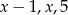 są długościami boków trójkąta równoramiennego. Oblicz
są długościami boków trójkąta równoramiennego. Oblicz  .
.
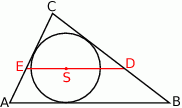
Przez środek 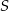 okręgu wpisanego w trójkąt
okręgu wpisanego w trójkąt 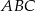 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 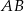 , która przecina boki
, która przecina boki 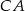 i
i 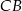 odpowiednio w punktach
odpowiednio w punktach 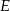 i
i 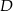 .
.
Wykaż, że 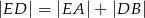 .
.
W trójkącie równobocznym 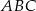 połączono środki wysokości otrzymując trójkąt
połączono środki wysokości otrzymując trójkąt  . Oblicz stosunek pól trójkątów
. Oblicz stosunek pól trójkątów  i
i 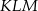 .
.
Punkty 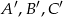 są środkami boków trójkąta
są środkami boków trójkąta 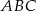 . Pole trójkąta
. Pole trójkąta 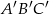 jest równe 4. Oblicz pole trójkąta
jest równe 4. Oblicz pole trójkąta 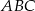 .
.
Wysokość trójkąta prostokątnego poprowadzona na przeciwprostokątną dzieli ją na odcinki długości 1 cm i 49 cm. Oblicz pole tego trójkąta.
Trójkąty prostokątne równoramienne  i
i  są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku
są położone tak, jak na poniższym rysunku (w obu trójkątach kąt przy wierzchołku 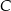 jest prosty). Wykaż, że
jest prosty). Wykaż, że 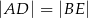 .
.
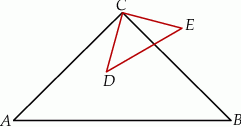
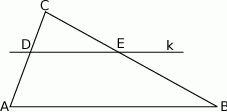
Prosta 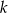 równoległa do boku
równoległa do boku 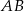 trójkąta
trójkąta 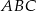 przecina boki
przecina boki 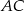 oraz
oraz 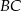 odpowiednio w punktach
odpowiednio w punktach 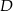 i
i 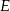 (zobacz rysunek). Wiadomo, że pole trójkąta
(zobacz rysunek). Wiadomo, że pole trójkąta 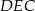 wynosi
wynosi 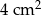 , zaś pole trapezu
, zaś pole trapezu 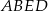 jest równe
jest równe 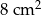 . Wykaż, że
. Wykaż, że 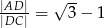 .
.
Oblicz sumę długości boków i pole trójkąta prostokątnego, w którym jedna z przyprostokątnych jest równa 10 cm, a druga jest o 2 cm krótsza od przeciwprostokątnej.
Podstawa trójkąta równoramiennego i środkowe poprowadzone z jej konców mają długość  . Oblicz długość wysokości poprowadzonej do podstawy.
. Oblicz długość wysokości poprowadzonej do podstawy.
Trójkąty 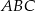 i
i 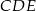 są równoboczne. Punkty
są równoboczne. Punkty 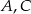 i
i 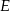 leżą na jednej prostej. Punkty
leżą na jednej prostej. Punkty 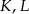 i
i 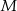 są środkami odcinków
są środkami odcinków 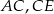 i
i 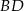 (zobacz rysunek). Wykaż, że punkty
(zobacz rysunek). Wykaż, że punkty 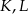 i
i 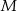 są wierzchołkami trójkąta równobocznego.
są wierzchołkami trójkąta równobocznego.
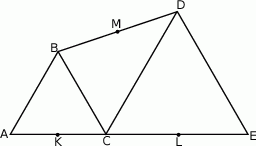
W trójkącie 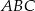 miara kąta
miara kąta 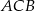 jest dwa razy większa od miary kąta
jest dwa razy większa od miary kąta 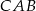 . Dwusieczna kąta
. Dwusieczna kąta 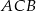 dzieli trójkąt
dzieli trójkąt 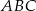 na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta
na dwa trójkąty. Uzasadnij, że jeden z otrzymanych trójkątów jest podobny do trójkąta  .
.

