Zestaw użytkownika nr 5244_1525
Zestaw użytkownika
nr 5244_1525
Dwudziestu sześciu uczniów klasy gimnazjalnej postanowiło wybrać się na czterodniową wycieczkę z trzema noclegami. Trasa przejazdu wynosiła łącznie 600 km. W biurze turystycznym uczniowie otrzymali następujące propozycje:
– cena jednego noclegu – 25 zł od osoby
– wyżywienie w ciągu jednego dnia (śniadanie, obiad, kolacja) – 30 zł od osoby
– bilety wejściowe do muzeum i przewodnik grupy dla całej wycieczki – 1200 zł
– cena 1 km przejazdu autokarem – 2,50 zł
Oblicz łączny koszt wycieczki dla całej grupy, jeśli pierwszego dnia uczniowie mają zamiar skorzystać tylko z obiadu i kolacji, czwartego dnia tylko ze śniadania. Oblicz koszt wycieczki na jednego ucznia.
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?
Drużyna żeglarska, płynąc po największym polskim jeziorze Śniardwy, odległość między dwiema przystaniami, która na mapie w skali 1:1 000 000 wynosi 5 cm, pokonała w czasie 2 godzin i 30 min. Oblicz średnią prędkość żaglówki.
Uprość wyrażenie 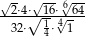 .
.
Wnuczek ma tyle miesięcy co dziadek lat. Razem maja 91 lat. Ile lat ma dziadek, a ile wnuczek?
Na zlecenie klienta makler ma kupić akcje spółek 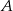 i
i 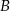 za 1000 zł. Cena jednej akcji spółki
za 1000 zł. Cena jednej akcji spółki 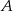 jest równa 4,25 zł, a jedna akcja spółki
jest równa 4,25 zł, a jedna akcja spółki 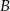 kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?
kosztuje 6,75 zł. Ile maksymalnie akcji każdego rodzaju makler może kupić, jeśli tańszych ma być o 10 więcej niż droższych?
Oblicz 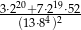 .
.
Za 4 jednakowe swetry i spodnie zapłacono 384 zł, a za sam sweter i spodnie 132 zł. Ile kosztuje sweter, a ile spodnie?
Zbieramy z Olkiem znaczki i wczoraj Olek mi powiedział, że ma już 155 znaczków angielskich, francuskich i hiszpańskich. Francuskich ma 2 razy więcej niż hiszpańskich, a angielskich o 39 mniej niz francuskich i hiszpańskich razem. To jednak niemożliwe, uzasadnij dlaczego Olek musiał się pomylić.
Dwóch braci pokonuje drogę z domu do szkoły pieszo. Młodszy potrzebuje na przebycie tej trasy 30 minut, a starszy 20 minut. Po ilu minutach starszy brat dogoni młodszego, jeśli wyjdzie z domu 5 minut po nim?
Cenę płaszcza zimowego obniżono wiosną o 15% i wówczas cena wynosiła 510 zł. Oblicz cenę płaszcza przed obniżką.
Która prędkość jest większa 50 km/h czy 30 m/s?
Książka kosztowała 12 zł, potem zdrożała o 20%, a następnie staniała o 25%. Oblicz cenę książki po tych zmianach.
Za normalne i ulgowe bilety kolejowe zapłacono 3250 zł. Stosunek liczby biletów normalnych do biletów ulgowych był równy 3:2 i jeden bilet ulgowy był o 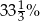 tańszy od biletu normalnego. Oblicz, ile zapłacono za bilety ulgowe.
tańszy od biletu normalnego. Oblicz, ile zapłacono za bilety ulgowe.
Oblicz: 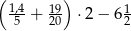 .
.
Ciocia jest 3 razy starsza od Basi. Za 16 lat Basia będzie miała tyle lat, ile ciocia przed 6 laty. Ile lat obecnie ma ciocia, a ile Basia?
W pewnej szkole 40 uczniów to członkowie SKS-u. Wśród nich 26 gra w siatkówkę, 25 pływa, a 27 jeździ na nartach. Jednocześnie pływa i gra w siatkówkę 15 uczniów, gra w siatkówkę i jeździ na nartach 16, a pływa i jeździ na nartach 18. Jeden uczeń nie zajmuje się sportem. Ilu uczniów uprawia wszystkie trzy dyscypliny sportowe? Ilu uczniów uprawia tylko jedną dyscyplinę sportową?
Pani Kowalska pobrała w banku kwotę 1000 zł w banknotach 20 zł i 50 zł. Łącznie otrzymała 32 banknoty. Ile otrzymała banknotów każdego rodzaju?
Piotrek kupił 3 rodzaje ciastek: duże, średnie i małe. Duże ciastko kosztuje 4 zł za sztukę, średnie po 2 zł, a małe po 1zł. Piotrek kupił łącznie 10 ciastek za które zapłacił 16 zł. Ile kupił dużych ciastek?
Uczniów pewnej szkoły ustawiono w kwadrat (tj. tyle samo rzędów, co uczniów w rzędzie). Następnie próbowano ich ustawić w prostokąt, zmniejszając liczbę rzędów o 4, a zwiększając o 5 liczbę uczniów w rzędzie. Okazało się, że brakuje 3 uczniów do wypełnienia tego prostokąta. Ilu uczniów liczyła ta szkoła?
Asi zerwał się naszyjnik. Trzecią część korali znalazła na podłodze, jedna czwarta w kieszeni, jedna piąta pod oparciem kanapy, a szósta część korali została na sznurku. Sześciu korali nie udało się jej odnaleźć. Oblicz, ile korali zostało na sznurku?
Do sklepu warzywno-owocowego zakupiono w hurtowni 250 kg pomidorów za 800 zł. Pierwszego dnia sprzedano 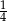 ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia
ilości kupionego towaru, drugiego dnia o 5,5 kg więcej niż pierwszego, a trzeciego dnia 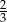 tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
tej ilości, którą sprzedano pierwszego i drugiego dnia razem. Ile kilogramów pomidorów zostało w sklepie? Jaki był zysk z trzydniowej sprzedaży warzyw, jeżeli cena detaliczna 1 kilograma pomidorów stanowi 1,25 ceny hurtowej?
Uczeń pomyślał pewną liczbę. Następnie dodał do niej 5, otrzymaną sumę podzielił przez 3, a otrzymany iloraz pomnożył przez 4. Potem od ostatniego wyniku odjął 6. Gdy tę różnicę podzielił przez 7, to otrzymał liczbę 2. Jaką liczbę pomyślał uczeń?
Oblicz odwrotność liczby 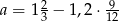 .
.
Janek przez 4 miesiące odkładał pieniądze na zakup roweru. W pierwszym miesiącu odłożył 30% potrzebnej kwoty, w drugim miesiącu o 60 zł mniej niż w pierwszym, w trzecim połowę wciąż brakującej sumy, a w czwartym 270 zł. Oblicz jaka była cena roweru.

