Zestaw użytkownika nr 5293_2220
FunkcjeMatura podstawowa
Wskaż 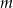 , dla którego funkcja liniowa
, dla którego funkcja liniowa 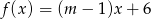 jest rosnąca
jest rosnąca
A) 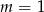 B)
B) 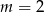 C)
C) 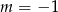 D)
D) 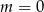
Dane są wielomiany 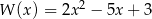 i
i 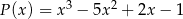 . Wielomian
. Wielomian 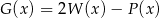 jest równy
jest równy
A) 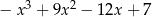 B)
B) 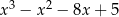 C)
C) 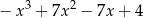 D)
D) 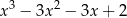
Pierwiastkami wielomianu stopnia trzeciego 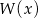 są liczby
są liczby 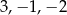 , a współczynnik stojący przy najwyższej potędze zmiennej
, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 3. Wielomian ten można zapisać w postaci
jest równy 3. Wielomian ten można zapisać w postaci
A) 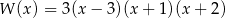
B) 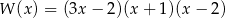
C) 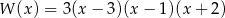
D) 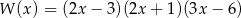
Funkcje 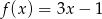 i
i 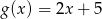 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 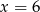 B)
B) 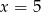 C)
C) 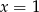 D)
D) 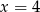
Dziedziną funkcji 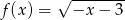 jest zbiór
jest zbiór
A) 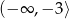 B)
B) 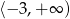 C)
C) 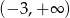 D)
D) 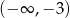
Dla kąta ostrego  spełniony jest warunek
spełniony jest warunek 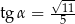 . Wówczas
. Wówczas
A) 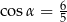 B)
B) 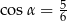 C)
C) 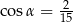 D)
D) 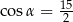
Kąt  jest ostry i
jest ostry i 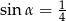 . Wówczas
. Wówczas
A) 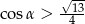 B)
B) 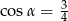 C)
C) 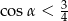 D)
D) 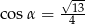
Wskaż funkcję, która nie przyjmuje wartości ujemnych
A) 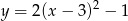 B)
B) 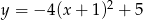 C)
C) 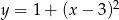 D)
D) 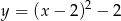
Wiadomo, że  jest kątem ostrym i
jest kątem ostrym i 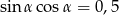 . Wynika stąd, że wartość wyrażenia
. Wynika stąd, że wartość wyrażenia 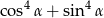 jest równa
jest równa
A) 0,25 B) 0,75 C) 1 D) 0,5
Funkcja 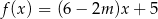 jest rosnąca, gdy
jest rosnąca, gdy
A) 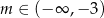 B)
B) 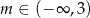 C)
C) 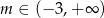 D)
D) 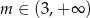
Funkcja 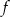 przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego
przyporządkowuje każdej liczbie naturalnej liczbę jej dzielników będących liczbami naturalnymi. Wobec tego 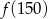 jest równe:
jest równe:
A) 10 B) 12 C) 13 D) 11
Dane są wielomiany 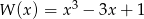 oraz
oraz 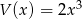 . Wielomian
. Wielomian 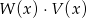 jest równy
jest równy
A) 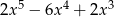 B)
B) 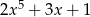 C)
C) 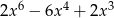 D)
D) 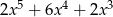
Wiadomo, że kąt  jest kątem ostrym i
jest kątem ostrym i 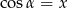 . Wtedy
. Wtedy 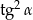 równa się
równa się
A) 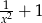 B)
B) 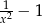 C)
C) 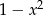 D)
D) 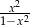
Kąt  jest kątem ostrym i
jest kątem ostrym i 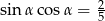 . Wówczas wyrażenie
. Wówczas wyrażenie 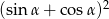 jest równe
jest równe
A) 1 B)  C)
C) 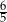 D)
D) 

