Zestaw użytkownika nr 5298_3256

Zestaw użytkownika
nr 5298_3256

Zadanie 1

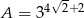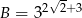Wykaż, że jeżeli 4√ 2+ 2 A = 3 i 2√ 2+3 B = 3 , to √ -- B = 9 A .

Zadanie 2

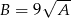Suma dwóch liczb jest równa 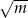√ -- m , a ich różnica jest równa 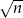√ -- n , gdzie 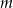i są dodatnimi liczbami całkowitymi. Wykaż, że iloczyn tych liczb jest liczbą wymierną.

Zadanie 3

Uprość wyrażenie 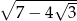∘ -----√--- 7 − 4 3 .

Zadanie 4

Wykaż, że liczba 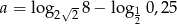√ - a = log2 28 − log12 0,25 jest liczbą wymierną.

Zadanie 5

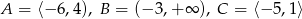Niech A = ⟨− 6,4), B = (− 3,+ ∞ ), C = ⟨− 5,1 ⟩ . Wyznacz zbiór (A ∖ C )∩ (B ∖ C ) .

Zadanie 6

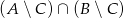Oblicz 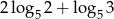2 log52 + log 53 .

Zadanie 7

Wykaż, że iloczyn trzech kolejnych liczb podzielnych przez 3 dzieli się przez 81.

Zadanie 8

Suma dwóch liczb jest równa 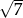√ -- 7 , a ich różnica 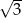√ -- 3 . Oblicz iloczyn tych liczb.

Zadanie 9

Oblicz wartość wyrażenia 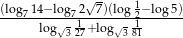(log 14−log 2√ 7)(log 1−log5) ---7-log√-71+-log√--21------ 327 3 81 .

Zadanie 10

Stosując wzory skróconego mnożenia rozłóż na czynniki wyrażenie 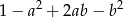1 − a2 + 2ab − b2 .

Zadanie 11

Wykaż, że suma kwadratów dwóch kolejnych liczb nieparzystych nie dzieli się przez 4.

Zadanie 12

Uzasadnij, że liczba 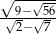√ 9−√-56 -√2−-√7- jest liczbą całkowitą.

Zadanie 13

Liczby dodatnie 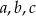a,b,c spełniają warunek: 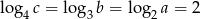log4c = lo g3b = log 2a = 2 . Oblicz √ ---- abc .

Zadanie 14

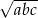Uprość wyrażenie 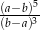(a−b-)5- (b−a )3 .

Zadanie 15

Doprowadź wyrażenie [ ( √ -) 3 ( √ - ) 2] ( ) x√3y- 2 + -√-x- : x 14 + y14 y x3 x8 y3 do najprostszej postaci.

Zadanie 16

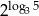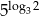Udowodnij, że liczby log 5 2 3 i log 2 5 3 są równe.

Zadanie 17

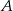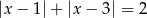Niech będzie zbiorem wszystkich liczb , które spełniają równość |x − 1|+ |x − 3 | = 2 . Niech 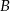będzie zbiorem wszystkich punktów na osi liczbowej, których suma odległości od punktów 4 i 6 jest niewiększa niż 4. Zaznacz na osi liczbowej zbiory 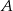i 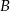oraz wszystkie punkty, które należą jednocześnie do 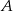i do .

Zadanie 18

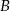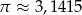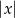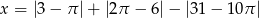Wiedząc, że π ≈ 3,1415 oblicz |x | , gdzie x = |3− π| + |2π − 6| − |31− 10π | .

Arkusz Wersja PDF