Zestaw użytkownika nr 5343_5761
Zestaw użytkownika
nr 5343_5761
O zdarzeniach 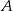 i
i 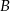 wiadomo, że
wiadomo, że 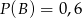 ,
, 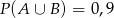 oraz
oraz 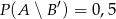 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 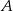 .
.
Zdarzenia losowe 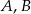 są zawarte w
są zawarte w 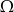 oraz
oraz 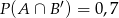 (
(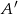 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 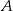 ,
, 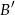 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 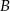 ). Wykaż, że
). Wykaż, że 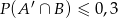 .
.
Prawdopodobieństwa zdarzeń 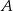 i
i 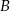 oraz zdarzeń do nich przeciwnych spełniają warunki:
oraz zdarzeń do nich przeciwnych spełniają warunki: 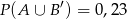 i
i 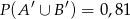 .
.
- Oblicz
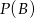 .
. - Wykaż, że jeżeli
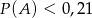 to
to 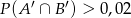 .
.
Wiadomo, że zdarzenia 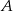 i
i 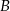 są niezależne oraz
są niezależne oraz 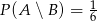 ,
, 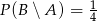 . Oblicz
. Oblicz 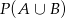 .
.
Dane są dwa takie zdarzenia 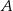 i
i 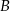 , że
, że 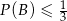 i
i 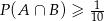 . Czy może zachodzić równość
. Czy może zachodzić równość 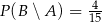 ? Odpowiedź uzasadnij.
? Odpowiedź uzasadnij.
O zdarzeniach 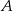 i
i 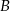 wiadomo, że
wiadomo, że 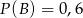 ,
, 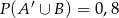 ,
, 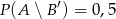 . Oblicz prawdopodobieństwo zdarzenia
. Oblicz prawdopodobieństwo zdarzenia 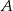 .
.
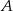 i
i 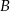 są takim zdarzeniami losowymi zawartymi w
są takim zdarzeniami losowymi zawartymi w 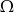 , że
, że 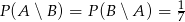 i
i 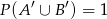 . Oblicz
. Oblicz 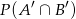 .
.
Zdarzenia losowe 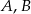 są zawarte w
są zawarte w 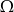 oraz
oraz 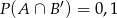 i
i 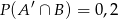 . Wykaż, że
. Wykaż, że 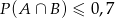 (
(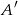 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 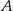 ,
, 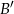 oznacza zdarzenie przeciwne do zdarzenia
oznacza zdarzenie przeciwne do zdarzenia 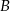 ).
).
Wiadomo, że 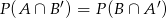 ,
, 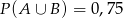 ,
, 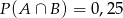 . Oblicz:
. Oblicz: 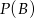 i
i 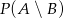 .
.
Wiadomo, że 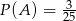 ,
, 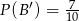 ,
, 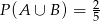 . Oblicz
. Oblicz 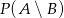 i
i 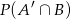 .
.
Spośród wyrazów skończonego ciągu arytmetycznego 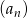 danego wzorem
danego wzorem 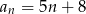 , gdzie
, gdzie 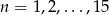 wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
wybieramy losowo 3. Oblicz prawdopodobieństwo, że iloczyn wybranych liczb jest podzielny przez 3.
Dany jest wielomian 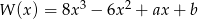 . Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
. Jednym pierwiastkiem wielomianu jest prawdopodobieństwo otrzymania co najmniej 2 razy orła w trzykrotnym rzucie monetą. Drugi pierwiastek jest równy prawdopodobieństwu wypadnięcia parzystej liczby oczek na każdej kostce w rzucie dwiema kostkami. Wyznacz trzeci pierwiastek wielomianu.
Ze zbioru 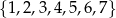 losujemy liczbę
losujemy liczbę  , a ze zbioru
, a ze zbioru 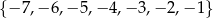 liczbę
liczbę 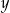 . Oblicz prawdopodobieństwo tego, że
. Oblicz prawdopodobieństwo tego, że 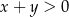 .
.
Spośród liczb 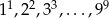 wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
wybieramy losowo trzy. Oblicz prawdopodobieństwo, że iloczyn tych liczb jest parzysty.
Na loterii jest  losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby
losów, w tym 4 wygrywające. Kupujemy 2 losy. Dla jakiej liczby  prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe
prawdopodobieństwo otrzymania co najmniej jednego losu wygrywającego jest równe 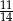 ?
?
Ze zbioru 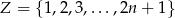 , gdzie
, gdzie 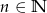 wylosowano równocześnie dwie liczby. Wyznacz
wylosowano równocześnie dwie liczby. Wyznacz  , tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od
, tak aby prawdopodobieństwo wylosowania liczb, których suma jest liczbą nieparzystą było większe od 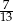 .
.
Ile maksymalnie kul zielonych można włożyć do urny, w której jest 7 kul czerwonych, aby prawdopodobieństwo wylosowania 2 kul różnokolorowych było większe lub równe 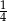 ?
?
Rzucono dwiema sześciennymi kostkami do gry i określono zdarzenia: 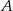 – na każdej kostce wypadła inna liczba oczek,
– na każdej kostce wypadła inna liczba oczek, 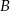 – suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia
– suma oczek jest mniejsza od 6. Oblicz prawdopodobieństwo zdarzenia 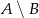 .
.
W urnie znajduje się  kul czarnych i
kul czarnych i 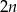 kul białych (
kul białych (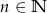 ,
, 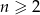 ). Losujemy jednocześnie dwie kule. Dla jakich
). Losujemy jednocześnie dwie kule. Dla jakich  prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?
prawdopodobieństwo wylosowania dwóch kul tego samego koloru jest większe od prawdopodobieństwa wylosowania dwóch kul różnych kolorów?

