Zestaw użytkownika nr 5411_9514
Zestaw użytkownika
nr 5411_9514
Dane są wielomiany 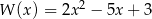 i
i 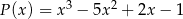 . Wielomian
. Wielomian 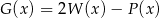 jest równy
jest równy
A) 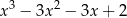 B)
B) 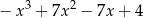 C)
C) 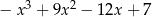 D)
D) 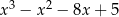
Pierwiastkami wielomianu stopnia trzeciego 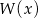 są liczby
są liczby 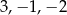 , a współczynnik stojący przy najwyższej potędze zmiennej
, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 3. Wielomian ten można zapisać w postaci
jest równy 3. Wielomian ten można zapisać w postaci
A) 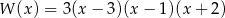
B) 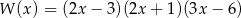
C) 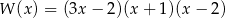
D) 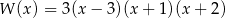
Dane są wielomiany 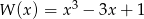 oraz
oraz 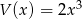 . Wielomian
. Wielomian 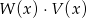 jest równy
jest równy
A) 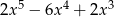 B)
B) 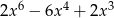 C)
C) 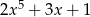 D)
D) 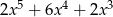
Wyraz wolny wielomianu 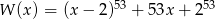 jest równy
jest równy
A) 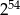 B) 0 C)
B) 0 C) 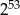 D) 53
D) 53
Wielomian 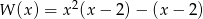 można zapisać w postaci
można zapisać w postaci
A) 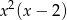 B)
B) 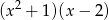 C)
C) 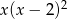 D)
D) 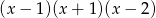
Wielomiany 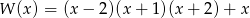 i
i 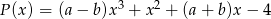 są równe. Z tego wynika, że
są równe. Z tego wynika, że
A) 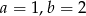 B)
B) 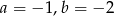 C)
C) 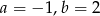 D)
D) 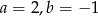
Stopień wielomianu 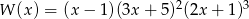 jest równy
jest równy
A) 4 B) 5 C) 6 D) 8
Suma współczynników wielomianu 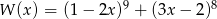 (po uporządkowaniu) jest równa
(po uporządkowaniu) jest równa
A) 0 B) 1 C) 2 D) 3
Wielomian 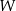 określony jest wzorem
określony jest wzorem 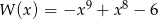 . Zatem
. Zatem 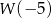 jest liczbą
jest liczbą
A) ujemną B) dodatnią C) niewymierną D) pierwszą
Po rozłożeniu wielomianu 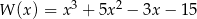 otrzymujemy
otrzymujemy
A) 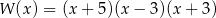
B) 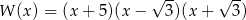
C) 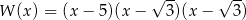
D) 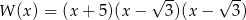
Wielomian 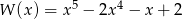
A) jest iloczynem wielomianów 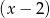 i
i 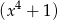
B) ma trzy miejsca zerowe
C) ma dwa miejsca zerowe
D) jest różnicą wielomianów 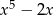 i
i 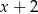
Rozwiąż równanie 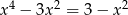 .
.
Rozwiąż równanie 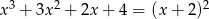 .
.
Rozwiąż równanie 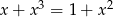 .
.
Rozwiąż równanie 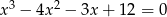 .
.
Rozwiąż równanie 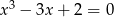 .
.
Dany jest wielomian 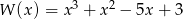 .
.
- Oblicz resztę z dzielenia tego wielomianu przez dwumian
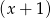 .
. - Oblicz miejsca zerowe tego wielomianu.
- Rozwiąż nierówność
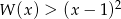 .
.

