Zestaw użytkownika nr 5484_3641
Zestaw użytkownika
nr 5484_3641
Zadanie 1
Dane są wielomiany 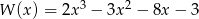 i
i 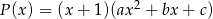 .
.
- Wyznacz współczynniki
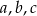 tak, aby
tak, aby 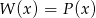 .
. - Przedstaw wielomian
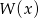 jako iloczyn wielomianów liniowych.
jako iloczyn wielomianów liniowych.
Zadanie 2
Wielomian 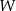 dany jest wzorem
dany jest wzorem 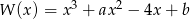 .
.
- Wyznacz
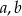 oraz
oraz  tak, aby wielomian
tak, aby wielomian 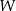 był równy wielomianowi
był równy wielomianowi 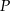 , gdy
, gdy 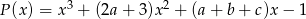 .
. - Dla
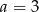 i
i 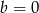 zapisz wielomian
zapisz wielomian 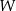 w postaci iloczynu trzech wielomianów stopnia pierwszego.
w postaci iloczynu trzech wielomianów stopnia pierwszego.
Zadanie 3
Wyznacz wartości  i
i 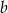 współczynników wielomianu
współczynników wielomianu 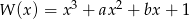 wiedząc, że
wiedząc, że 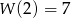 oraz, że reszta z dzielenia
oraz, że reszta z dzielenia 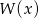 przez
przez 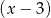 jest równa 10.
jest równa 10.
Zadanie 4
Pierwiastkami wielomianu 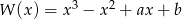 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
- Oblicz
 i
i 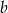 .
. - Zapisz wielomian w postaci czynników liniowych.
Zadanie 5
Rozwiąż równanie 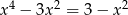 .
.
Zadanie 6
Miejscem zerowym wielomianu 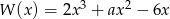 jest liczba (-1).
jest liczba (-1).
- Oblicz
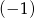 .
. - Wyznacz pozostałe miejsca zerowe
 .
.
Zadanie 7
Rozwiąż równanie 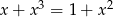 .
.
Zadanie 8
Liczba 3 jest pierwiastkiem wielomianu 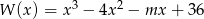 . Wyznacz parametr
. Wyznacz parametr 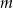 i pozostałe pierwiastki tego wielomianu.
i pozostałe pierwiastki tego wielomianu.
Zadanie 9
Dany jest wielomian 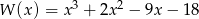 .
.
- Wyznacz pierwiastki tego wielomianu.
- Sprawdź, czy wielomiany
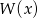 i
i 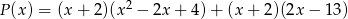 są równe.
są równe. - Uzasadnij, że jeśli
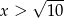 , to
, to 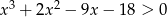 .
.

