Zestaw użytkownika nr 5487_2710
Prawdopodobieństwo 2
Na loterii jest 12 losów, z których 8 jest przegrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że wygramy nagrodę jest równe
A) 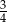 B)
B)  C)
C) 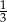 D)
D) 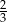
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A) 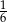 B)
B) 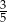 C)
C)  D)
D) 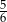
Ze zbioru 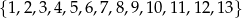 losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
losujemy jedną liczbę. Prawdopodobieństwo wylosowania liczby pierwszej jest równe
A) 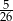 B)
B) 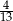 C)
C) 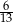 D)
D) 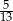
Ze zbioru dwucyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 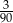 B)
B) 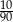 C)
C) 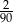 D)
D) 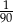
Z talii 24 kart (od dziewiątek) losujemy jedną. Prawdopodobieństwo, że wylosujemy waleta lub trefla, jest równe
A)  B)
B) 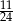 C)
C) 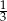 D)
D) 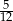
Z talii 52 kart losujemy jedną. Prawdopodobieństwo, że wylosujemy damę lub pika, jest równe
A) 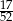 B)
B) 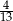 C)
C) 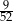 D)
D) 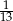
O zdarzeniach losowych 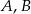 wiadomo, że:
wiadomo, że: 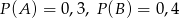 i
i 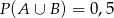 . Prawdopodobieństwo iloczynu zdarzeń
. Prawdopodobieństwo iloczynu zdarzeń 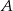 i
i 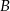 spełnia warunek
spełnia warunek
A) 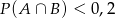 B)
B) 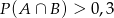 C)
C) 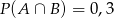 D)
D) 
W pudełku znajdują się tylko kule białe i czarne. Stosunek liczby kul czarnych do liczby kul białych jest równy 4:5. Z pudełka losujemy jedną kulę. Prawdopodobieństwo wylosowania białej kuli jest równe
A)  B)
B)  C)
C)  D)
D) 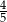
Rzucamy dwiema kostkami do gry. Jeśli 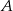 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10”, a 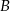 oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 11” to
A) 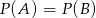 B)
B) 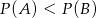 C)
C) 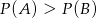 D)
D) 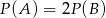
Rzucamy dwiema kostkami do gry. Jeśli 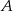 oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”, a
oznacza zdarzenie „suma wyrzuconych oczek jest równa 6”, a 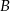 oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
oznacza zdarzenie „suma wyrzuconych oczek jest równa 10” to
A) 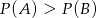 B)
B) 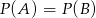 C)
C) 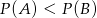 D)
D) 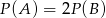
Rzucamy dwiema sześciennymi kostkami do gry. Prawdopodobieństwo tego, że suma wyrzuconych oczek wyniesie co najwyżej 9, jest równe
A) 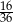 B)
B) 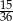 C)
C) 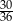 D)
D) 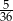
Prawdopodobieństwa zdarzeń 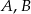 oraz zdarzeń przeciwnych
oraz zdarzeń przeciwnych 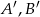 spełniają równości
spełniają równości 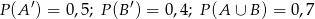 . Wtedy
. Wtedy 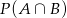 jest równe
jest równe
A) 0,3 B) 0,2 C) 0,4 D) 0,1
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadną co najwyżej 3 oczka, jest równe
A) 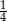 B)
B) 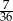 C)
C) 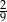 D)
D) 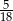
Rzucamy dwukrotnie sześcienną kostką do gry. Prawdopodobieństwo zdarzenia, że na każdej kostce wypadnie co najmniej 5 oczek, jest równe
A) 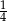 B)
B) 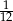 C)
C) 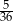 D)
D) 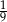
Ze zbioru cyfr 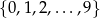 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
A)  B)
B)  C)
C) 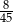 D)
D) 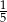
Rzucamy dwa razy sześcienną kostką do gry. Prawdopodobieństwo wyrzucenia co najmniej raz liczby oczek większej od 4 jest równe
A) 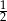 B)
B) 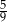 C)
C) 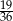 D)
D) 
Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub waleta lub króla, jest równe
A) 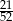 B)
B) 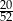 C)
C) 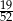 D)
D) 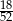
Z talii 52 kart losujemy jedną. Prawdopodobieństwo tego, że wylosujemy kartę trefl lub pik lub waleta, jest równe
A) 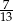 B)
B) 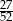 C)
C) 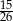 D)
D) 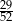
W kapeluszu znajdują się króliki białe i szare. Prawdopodobieństwo wyciągnięcia z kapelusza królika szarego jest równe 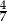 . Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
. Zatem prawdopodobieństwo wyciągnięcia z kapelusza królika białego jest równe
A) 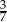 B) 0,75 C)
B) 0,75 C)  D)
D) 
Prawdopodobieństwo, że przy rzucie pięcioma monetami otrzymamy co najmniej trzy reszki, jest równe
A) 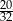 B)
B) 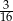 C)
C) 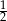 D)
D)