Zestaw użytkownika nr 5567_7118
FUNKCJE LINIOWE18 Kwietnia 2012Czas pracy: 45 min.Suma punktów: 29
Wyznacz miejsca zerowe funkcji
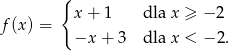
Napisz wzór funkcji liniowej o współczynniku kierunkowym 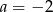 , której wykres przecina oś
, której wykres przecina oś 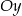 w punkcie
w punkcie 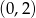 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
O funkcji liniowej 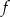 wiadomo, że
wiadomo, że 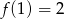 oraz, że do wykresu tej funkcji należy punkt
oraz, że do wykresu tej funkcji należy punkt 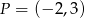 . Wyznacz wzór funkcji
. Wyznacz wzór funkcji 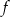 .
.
Wskaż 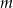 , dla którego funkcja liniowa
, dla którego funkcja liniowa 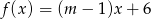 jest rosnąca
jest rosnąca
A) 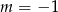 B)
B) 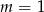 C)
C) 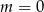 D)
D) 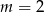
Funkcje 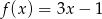 i
i 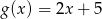 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 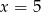 B)
B) 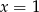 C)
C) 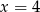 D)
D) 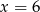
Dana jest funkcja liniowa określona wzorem 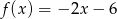 . Wartości ujemne przyjmuje dla:
. Wartości ujemne przyjmuje dla:
A) 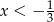 B)
B) 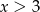 C)
C) 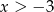 D)
D) 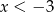
Funkcją malejącą jest funkcja
A) 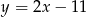 B)
B) 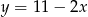 C)
C) 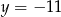 D)
D) 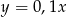
Funkcja 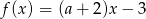 nie ma miejsc zerowych. Wobec tego liczba
nie ma miejsc zerowych. Wobec tego liczba  jest równa
jest równa
A) -2 B) 3 C) 0 D) -3
Miejscem zerowym funkcji 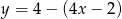 jest:
jest:
A) 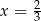 B)
B) 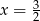 C)
C) 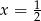 D)
D) 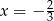
Wykres funkcji liniowej 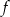 przecina osie
przecina osie 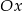 i
i 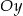 układu współrzędnych odpowiednio w punktach
układu współrzędnych odpowiednio w punktach 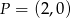 oraz
oraz 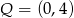 .
.
- Wyznacz wzór funkcji
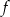 .
. - Sprawdź, czy dla argumentu
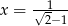 wartość funkcji
wartość funkcji 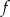 wynosi
wynosi 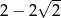 .
.
Na rysunku przedstawiony jest wykres funkcji liniowej 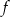 .
.
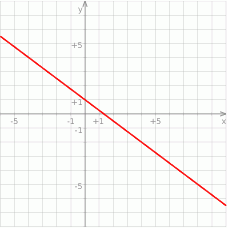
Funkcja 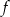 jest określona wzorem
jest określona wzorem
A) 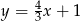 B)
B) 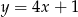 C)
C) 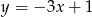 D)
D) 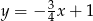
Do wykresu funkcji 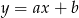 należą punkty
należą punkty 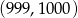 oraz
oraz 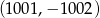 . Wówczas
. Wówczas
A) 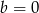 B)
B) 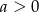 C)
C) 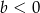 D)
D) 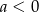
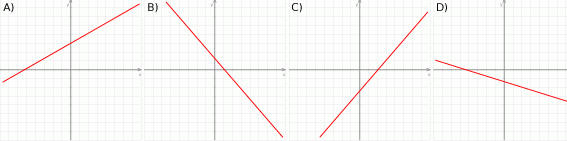
Na którym rysunku przedstawiono wykres funkcji liniowej 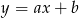 takiej, że
takiej, że 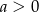 i
i 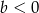 ?
?
Jeżeli wykres funkcji 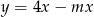 nie ma punktów wspólnych z prostą
nie ma punktów wspólnych z prostą 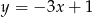 to
to
A) 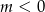 B)
B) 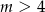 C)
C) 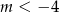 D)
D) 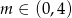
Funkcja liniowa, której wykres jest równoległy do wykresu funkcji 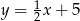 ma wzór:
ma wzór:
A) 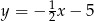 B)
B) 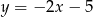 C)
C) 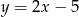 D)
D) 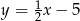
Punkt 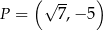 należy do wykresu funkcji
należy do wykresu funkcji 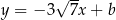 . Parametr
. Parametr 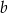 jest równy
jest równy
A) 16 B) 26 C) -16 D) -26
Do wykresu funkcji liniowej 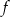 należą punkty
należą punkty 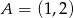 i
i 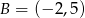 . Funkcja
. Funkcja 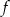 ma wzór
ma wzór
A) 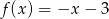 B)
B) 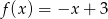 C)
C) 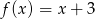 D)
D) 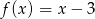
Zależność między temperaturą wyrażoną w stopniach Fahrenheita, a wyrażoną w stopniach Celsjusza jest zależnością liniową.
- Znajdź tę zależność wiedząc ze
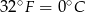 , a
, a 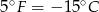 .
. - 22 lipca w San Diego temperatura o godzinie
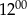 była o
była o 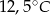 wyższa niż temperatura o godzinie
wyższa niż temperatura o godzinie 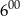 . Wyraź wzrost temperatury w stopniach Fahrenheita.
. Wyraź wzrost temperatury w stopniach Fahrenheita.

