Zestaw użytkownika nr 5627_5159
Zestaw użytkownika
nr 5627_5159
Dziedziną funkcji 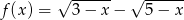 jest zbiór
jest zbiór
A) 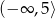 B)
B) 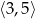 C)
C) 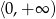 D)
D) 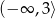
Dla jakich liczb naturalnych wyrażenie 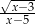 ma sens liczbowy?
ma sens liczbowy?
A) 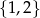 B)
B) 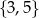 C)
C) 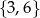 D)
D) 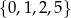
Funkcja 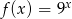 dla argumentu
dla argumentu 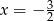 przyjmuje wartość
przyjmuje wartość
A) 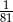 B)
B) 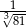 C) 27 D)
C) 27 D) 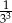
Funkcja 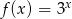 nie przyjmuje wartości
nie przyjmuje wartości
A) 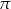 B)
B) 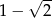 C)
C) 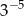 D)
D) 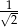
Miejscem zerowym funkcji
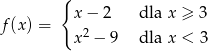
jest liczba
A) 2 B) -3 C) 3 D) 9
Zbiorem wartości funkcji 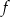 jest przedział
jest przedział 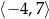 . Zatem zbiorem wartości funkcji
. Zatem zbiorem wartości funkcji 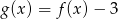 jest przedział
jest przedział
A) 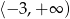 B)
B) 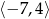 C)
C) 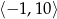 D)
D) 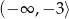
Funkcja 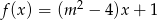 jest funkcją stałą. Wynika stąd, że
jest funkcją stałą. Wynika stąd, że
A) 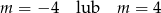 B)
B) 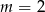 C)
C) 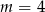 D)
D) 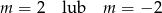
Funkcje 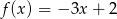 i
i 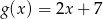 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 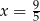 B)
B) 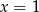 C)
C) 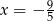 D)
D) 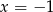
Funkcją malejącą jest funkcja
A) 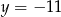 B)
B) 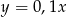 C)
C) 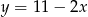 D)
D) 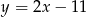
Funkcja 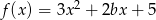 maleje w przedziale
maleje w przedziale 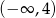 i rośnie w przedziale
i rośnie w przedziale 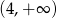 . Wynika stąd, że
. Wynika stąd, że
A) 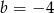 B)
B) 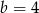 C)
C) 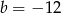 D)
D) 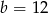
Zbiorem wartości funkcji kwadratowej 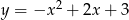 jest przedział
jest przedział
A) 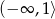 B)
B) 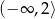 C)
C) 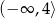 D)
D) 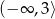
Na rysunku jest przedstawiony wykres funkcji 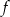 .
.
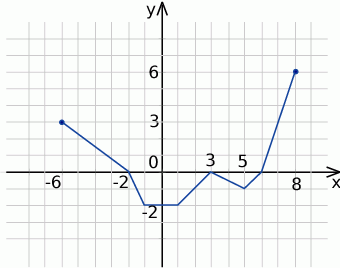
- Podaj dziedzinę funkcji
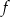 .
. - Podaj wszystkie miejsca zerowe funkcji
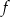 .
. - Odczytaj wartość funkcji
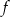 dla argumentu
dla argumentu 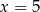 .
. - Podaj zbiór wartości funkcji
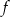 .
. - Podaj maksymalny przedział o długości 3, w którym funkcja
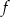 jest rosnąca.
jest rosnąca. - Zapisz w postaci sumy przedziałów zbiór wszystkich argumentów, dla których funkcja
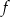 przyjmuje wartości ujemne.
przyjmuje wartości ujemne.
Wyznacz najmniejszą i największą wartość funkcji 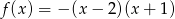 w przedziale
w przedziale 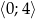 .
.
Dane są dwie funkcje kwadratowe 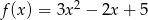 i
i 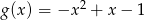 . Wyznacz największą wartość funkcji
. Wyznacz największą wartość funkcji 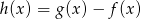 .
.
Dana jest funkcja liniowa 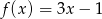 .
.
- Rozwiąż nierówność
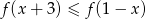 .
. - Podaj maksymalne przedziały monotoniczności funkcji
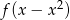 .
.
Wyznacz wartość funkcji 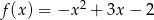 dla argumentu
dla argumentu 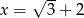 .
.

