Zestaw użytkownika nr 5636_8179
Zestaw użytkownika
nr 5636_8179
Wyznacz współrzędne wierzchołków trójkąta jeżeli środki jego boków mają współrzędne: 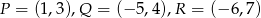 .
.
Dla jakich wartości parametru  odległość punktu
odległość punktu 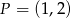 od prostej
od prostej 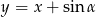 jest mniejsza lub równa
jest mniejsza lub równa 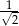 .
.
Podstawą trójkąta równoramiennego jest odcinek o końcach w punktach 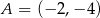 oraz
oraz 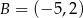 . Jedno z jego ramion zawiera się w prostej o równaniu
. Jedno z jego ramion zawiera się w prostej o równaniu 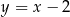 . Oblicz współrzędne trzeciego wierzchołka trójkąta.
. Oblicz współrzędne trzeciego wierzchołka trójkąta.
Dany jest punkt 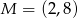 . Wyznacz równanie takiej prostej
. Wyznacz równanie takiej prostej 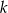 , do której należy punkt
, do której należy punkt 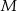 , że na ujemnej półosi
, że na ujemnej półosi 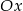 i dodatniej półosi
i dodatniej półosi 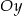 układu
układu 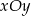 prosta ta wyznacza odcinki
prosta ta wyznacza odcinki 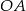 i
i 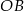 , których suma długości jest równa 6. Oblicz obwód trójkąta
, których suma długości jest równa 6. Oblicz obwód trójkąta 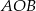 .
.
Dane są punkty 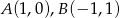 . Punkt
. Punkt 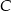 należy do okręgu o równaniu
należy do okręgu o równaniu 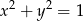 . Znajdź współrzędne punktu
. Znajdź współrzędne punktu 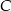 , tak aby pole trójkąta było największe. Oblicz to pole.
, tak aby pole trójkąta było największe. Oblicz to pole.
Ile punktów wspólnych ma prosta 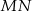 z okręgiem
z okręgiem 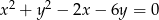 jeśli
jeśli 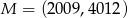 oraz
oraz 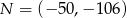 .
.
Punkty 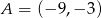 i
i 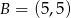 są wierzchołkami trójkąta prostokątnego
są wierzchołkami trójkąta prostokątnego 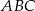 , w którym
, w którym 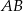 jest przeciwprostokątną. Wyznacz współrzędne wierzchołka
jest przeciwprostokątną. Wyznacz współrzędne wierzchołka 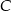 wiedząc, że leży on na osi
wiedząc, że leży on na osi 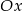 .
.
Dla jakich wartości parametru 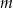 równanie
równanie 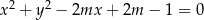 opisuje okrąg?
opisuje okrąg?
- Podaj wspórzędne środka i długość promienia okręgu.
- Dla jakich wartości parametru
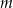 okrąg ten jest styczny do prostej o równaniu
okrąg ten jest styczny do prostej o równaniu 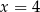 ?
?
Dana jest prosta 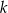 o równaniu
o równaniu 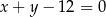 oraz punkt
oraz punkt 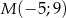 wyznacz na prostej
wyznacz na prostej 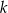 takie punkty
takie punkty 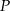 i
i 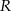 aby
aby 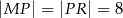 .
.
Wyznacz równanie takiej prostej przechodzącej przez punkt 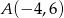 , która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
, która wraz z osiami układu współrzędnych ogranicza trójkąt o polu równym 2.
W okrąg o równaniu 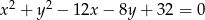 wpisano trójkąt równoboczny
wpisano trójkąt równoboczny 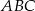 w którym
w którym 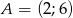 . Oblicz współrzędne pozostałych wierzchołków trójkąta.
. Oblicz współrzędne pozostałych wierzchołków trójkąta.
Punkt 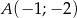 jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej
jest wierzchołkiem rombu, którego jeden z boków zawiera się w prostej 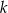 o równaniu
o równaniu 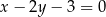 . Środkiem symetrii tego rombu jest punkt
. Środkiem symetrii tego rombu jest punkt 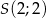 . Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
. Oblicz współrzędne pozostałych wierzchołków rombu i oblicz jego pole.
Dany jest okrąg 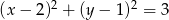 . Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę
. Oblicz pole rombu opisanego na tym okręgu, jeśli kąt ostry rombu ma miarę 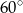 .
.
Jeden z boków kwadratu 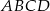 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 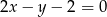 . Wierzchołek
. Wierzchołek 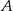 ma współrzędne
ma współrzędne 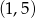 .
.
- Znajdź współrzędne pozostałych wierzchołków.
- Oblicz pole kwadratu
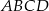 .
.
Dla jakich wartości parametru 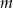 proste
proste 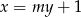 oraz
oraz 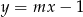 przecinają się w jednym punkcie, który leży poniżej prostej
przecinają się w jednym punkcie, który leży poniżej prostej 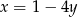 ?
?
Na paraboli o równaniu 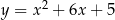 znajdź współrzędne punktu
znajdź współrzędne punktu 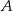 , którego odległość od prostej o równaniu
, którego odległość od prostej o równaniu 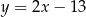 jest najmniejsza.
jest najmniejsza.
Znajdź równanie krzywej, którą tworzą wszystkie punkty jednakowo odległe od okręgu 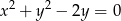 i od prostej
i od prostej 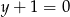 .
.

