Zadanie nr 5661402
Funkcja 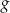 jest określona wzorem
jest określona wzorem 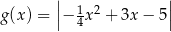 dla każdego
dla każdego 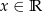 . Fragment wykresu funkcji
. Fragment wykresu funkcji 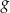 w kartezjańskim układzie współrzędnych
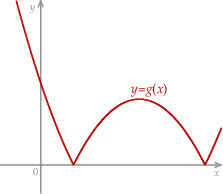
w kartezjańskim układzie współrzędnych 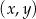 przedstawiono na rysunku (jednostki pominięto).
przedstawiono na rysunku (jednostki pominięto).
Wyznacz zbiór wszystkich wartości, jakie funkcja 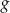 przyjmuje w przedziale
przyjmuje w przedziale ![[9,11]](https://img.zadania.info/zad/5661402/HzadT7x.gif) .
.
Rozwiązanie
Sprawdźmy jakie są miejsca zerowe funkcji 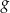 .
.
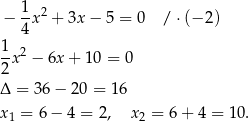
Stąd
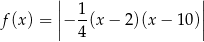
i pierwsza współrzędna wierzchołek paraboli poda wartością bezwzględną jest równa
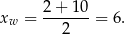
W takim razie większe miejsce zerowe funkcji 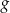 znajduje się w przedziale
znajduje się w przedziale ![[9,11]](https://img.zadania.info/zad/5661402/HzadR5x.gif) , a wierzchołek jest poza tym przedziałem. Zatem zbiorem wartości funkcji
, a wierzchołek jest poza tym przedziałem. Zatem zbiorem wartości funkcji 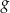 na tym przedziale będzie jeden z przedziałów:
na tym przedziale będzie jeden z przedziałów: ![[0,g (9)]](https://img.zadania.info/zad/5661402/HzadR7x.gif) lub
lub ![[0,g(11 )]](https://img.zadania.info/zad/5661402/HzadR8x.gif) . Pozostało sprawdzić, który z nich.
. Pozostało sprawdzić, który z nich.
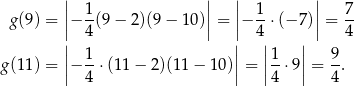
Zbiorem wartości funkcji 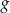 jest więc przedział
jest więc przedział
![[ 9] [0,g(11 )] = 0,-- . 4](https://img.zadania.info/zad/5661402/HzadR11x.gif)
Odpowiedź: ![[ ] 0, 94](https://img.zadania.info/zad/5661402/HzadR12x.gif)

