Zestaw użytkownika nr 5772_9988

Zestaw użytkownika
nr 5772_9988

Zadanie 1

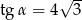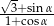Wiedząc, że jest kątem ostrym oraz √ -- tg α = 4 3 oblicz wartość wyrażenia √ - --3+sinα 1+cosα .

Zadanie 2

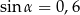Oblicz wartości pozostałych funkcji trygonometrycznych kąta ostrego jeżeli sin α = 0 ,6 .

Zadanie 3

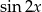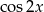Wyznacz sin 2x i cos2x jeśli wiadomo że 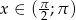π- x ∈ ( 2;π) i tgx = − 5 .

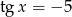Zadanie 4

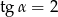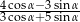Wiedząc, że jest kątem ostrym i tgα = 2 , oblicz wartość wyrażenia 43-cocossαα−+-35ssininαα .

Zadanie 5

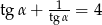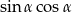Wiedząc, że jest kątem ostrym i -1- tgα + tgα = 4 oblicz sin α cosα .

Zadanie 6

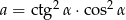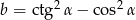Porównaj liczby: 2 2 a = ctg α ⋅cos α i 2 2 b = ctg α− cos α , jeżeli ∘ α = 60 .

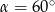Zadanie 7

Sprawdź tożsamość: 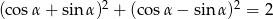2 2 (cos α+ sin α) + (cos α− sin α) = 2 .

Zadanie 8

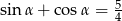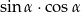Wiedząc, że 5 sin α+ cosα = 4 , oblicz sin α⋅co sα .

Zadanie 9

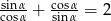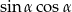Kąt jest ostry i -sinα cosα cosα + sinα = 2 . Oblicz wartość wyrażenia sin αco sα .

Zadanie 10

Sprawdź, czy prawdziwa jest następująca tożsamość 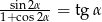-sin2α-- 1+cos2α = tgα . Podaj konieczne założenia.

Zadanie 11

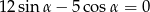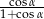Kąta jest ostry oraz 12 sin α − 5 cosα = 0 . Oblicz -cosα-- 1+ cosα .

Zadanie 12

Oblicz wartość wyrażenia 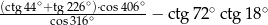(ctg44∘+tg226∘)⋅cos406∘ ∘ ∘ cos316∘ − ctg 72 ctg 18 .

Zadanie 13

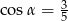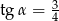Wykaż, że nie istnieje kąt , taki, że 3 cos α = 5 i 3 tgα = 4 .

Zadanie 14

Wyznacz najmniejszą wartość funkcji 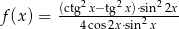(ctg2x−tg2x)⋅sin22x f(x) = ---4cos2x⋅sin2x---- .

Zadanie 15

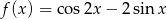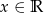Wyznacz zbiór wartości funkcji: f (x) = cos 2x− 2sin x , gdzie x ∈ R .

Arkusz Wersja PDF