Zadanie nr 5774571
Nieskończony ciąg geometryczny 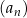 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 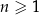 . Suma wszystkich wyrazów ciągu
. Suma wszystkich wyrazów ciągu 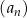 o numerach nieparzystych jest równa 16, tj.
o numerach nieparzystych jest równa 16, tj.
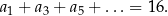
Ponadto 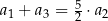 . Wyznacz wzór ogólny na n–ty wyraz ciągu
. Wyznacz wzór ogólny na n–ty wyraz ciągu 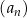 .
.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

