Zestaw użytkownika nr 5794_8133
Stereometria sprawdzian zaliczenieCzas pracy: 90 min.Suma punktów: 37
Promień podstawy walca zwiększamy trzy razy, a jego wysokość zmniejszamy trzy razy. Wówczas objętość walca
A) zwiększy się trzy razy
B) zwiększy się o trzy
C) nie zmieni się
D) zmniejszy się trzy razy
Powierzchnia sześcianu wynosi 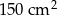 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 5,5 cm B) 5 cm C) 4 cm D) 6 cm
Przekątna prostopadłościanu o wymiarach 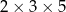 ma długość
ma długość
A) 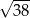 B)
B) 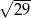 C)
C) 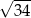 D)
D) 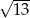
Przekrój osiowy stożka jest trójkątem równoramiennym o stosunku ramienia do podstawy 3:2. Tworząca stożka tworzy z podstawą kąt  , taki, że
, taki, że
A) 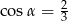 B)
B) 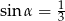 C)
C) 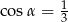 D)
D) 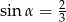
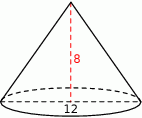
Objętość stożka o wysokości 8 i średnicy podstawy 12 jest równa
A) 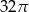 B)
B) 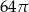 C)
C) 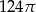 D)
D) 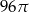
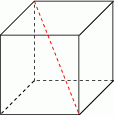
Krawędź sześcianu ma długość 9. Długość przekątnej tego sześcianu jest równa:
A) 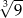 B)
B) 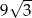 C)
C) 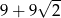 D)
D) 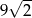
Pole powierzchni całkowitej czworościanu foremnego jest równe 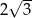 . Suma długości krawędzi tego czworościanu jest równa
. Suma długości krawędzi tego czworościanu jest równa
A) 12 B) 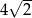 C)
C) 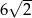 D)
D) 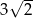
Trójkąt równoboczny o boku długości 4 cm obrócono wokół prostej zawierającej wysokość trójkąta. Objętość powstałej bryły jest równa:
A) 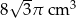 B)
B) 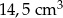 C)
C) 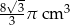 D)
D) 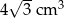
Ostrosłup ma 18 wierzchołków. Liczba wszystkich krawędzi tego ostrosłupa jest równa
A) 18 B) 27 C) 34 D) 11
Średnica kuli 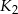 jest dwa razy dłuższa od średnicy kuli
jest dwa razy dłuższa od średnicy kuli 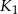 . Ile razy objętość kuli
. Ile razy objętość kuli 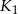 jest mniejsza od objętości kuli
jest mniejsza od objętości kuli 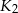 ?
?
A) 4 razy B) 3 razy C) 8 razy D) 2 razy
Trójkąt prostokątny o przyprostokątnych długości 8 i 6 obrócono wokół dłuższej przyprostokątnej. Pole powierzchni bocznej tak otrzymanej bryły jest równe
A) 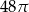 B)
B) 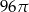 C)
C) 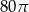 D)
D) 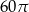
Pole powierzchni bocznej stożka o kącie rozwarcia 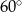 i wysokości
i wysokości 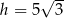 jest równe
jest równe
A) 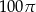 B)
B) 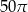 C)
C) 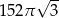 D)
D) 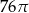
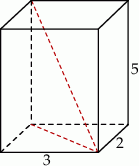
Podstawą ostrosłupa 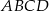 jest trójkąt
jest trójkąt 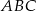 . Krawędź
. Krawędź 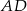 jest wysokością ostrosłupa (zobacz rysunek).
jest wysokością ostrosłupa (zobacz rysunek).
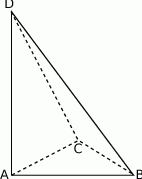
Oblicz objętość ostrosłupa  , jeśli wiadomo, że
, jeśli wiadomo, że 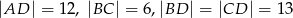 .
.
Pole powierzchni bocznej stożka jest cztery razy większe od pola podstawy. Obwód przekroju osiowego stożka jest równy 30. Oblicz objętość tego stożka
Powierzchnia boczna walca po rozwinięciu jest prostokątem, którego przekątna ma długość 18 cm i tworzy z bokiem odpowiadającym wysokości walca kąt o mierze 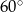 . Oblicz objętość walca.
. Oblicz objętość walca.
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.
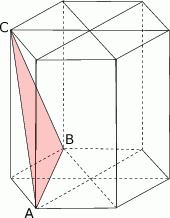
W graniastosłupie prawidłowym sześciokątnym płaszczyzna  zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem
zawierająca przekątne sąsiednich ścian bocznych, wychodzących z tego samego wierzchołka, jest nachylona do podstawy graniastosłupa pod kątem 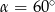 . Pole przekroju graniastosłupa tą płaszczyzną równa się
. Pole przekroju graniastosłupa tą płaszczyzną równa się 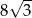 . Zaznacz na poniższym rysunku kąt
. Zaznacz na poniższym rysunku kąt  . Oblicz objętość tego graniastosłupa.
. Oblicz objętość tego graniastosłupa.
Krawędź boczna ostrosłupa prawidłowego czworokątnego ma długość 4 cm i jest nachylona do płaszczyzny podstawy pod kątem 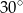 . Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.
. Oblicz długość krawędzi sześcianu, którego objętość jest równa objętości tego ostrosłupa.

