Zestaw użytkownika nr 6028_3878

Zestaw użytkownika
nr 6028_3878

Zadanie 1
(5 pkt)

Oblicz objętość i pole powierzchni całkowitej ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 2, a krawędź boczna długość 6.

Zadanie 2
(5 pkt)

Podstawą graniastosłupa jest trójkąt prostokątny, w którym przeciwprostokątna ma długość 8 cm, a jeden z kątów ma miarę 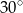30∘ . Powierzchnia boczna tego graniastosłupa po rozwinięciu na płaszczyznę jest kwadratem. Oblicz pole powierzchni całkowitej i objętość tego graniastosłupa.

Zadanie 3
(5 pkt)

W kulę o promieniu długości 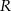R wpisano walec o największej objętości. Wyznacz stosunek objętości kuli do objętości tego walca.

Zadanie 4
(5 pkt)

Trójkąt prostokątny o przyprostokątnych długości 12 i 7 obraca się wokół przeciwprostokątnej. Oblicz promień kuli wpisanej w otrzymaną bryłę.

Zadanie 5
(5 pkt)

Objętość graniastosłupa prawidłowego trójkątnego jest równa 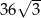√ -- 36 3 , a pole powierzchni bocznej tego graniastosłupa jest równe 72. Oblicz długość krawędzi podstawy oraz długość wysokości tego graniastosłupa.

Zadanie 6
(5 pkt)

Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.

Zadanie 7
(5 pkt)

Do naczynia w kształcie odwróconego stożka wrzucono kulkę o promieniu 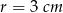r = 3 cm . Oceń, czy kulka będzie wystawać nad brzeg naczynia. Uzasadnij odpowiedź wykonując odpowiednie obliczenia, jeżeli wiadomo, że wysokość stożka wynosi 12 cm a promień podstawy 4 cm.

Zadanie 8
(5 pkt)

Przekątna przekroju osiowego walca ma długość 5 cm i jest nachylona do płaszczyzny podstawy pod kątem 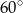60 ∘ . Jaką długość ma promień podstawy tego walca? Jaka jest jego wysokość?

Zadanie 9
(5 pkt)

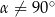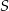W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę r wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna r z płaszczyzną podstawy graniastosłupa tworzy kąt o mierze α ⁄= 90∘ . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę r jest równe S . Oblicz objętość graniastosłupa.

Zadanie 10
(5 pkt)

Trapez prostokątny o podstawach długości 4 i 5 oraz kącie ostrym równym 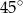45 ∘ obraca się wokół krótszej podstawy. Oblicz objętość otrzymanej bryły.

Zadanie 11
(5 pkt)

Tangens kąta nachylenia ściany bocznej do płaszczyzny podstawy ostrosłupa prawidłowego czworokątnego jest równy 23 . Oblicz tangens nachylenia krawędzi bocznej do płaszczyzny podstawy tego ostrosłupa.

Zadanie 12
(5 pkt)

Oblicz sinus kąta między przekątną sześcianu a jego płaszczyzną podstawy.

Zadanie 13
(5 pkt)

W stożek o promieniu podstawy długości 9 i wysokości 12 wpisano walec, w ten sposób, że jedna podstawa walca zawiera się w podstawie stożka, a brzeg jego drugiej podstawy zawiera się w powierzchni bocznej stożka. Oblicz długość promienia podstawy i długość wysokości walca, wiedząc że pole powierzchni bocznej walca wynosi 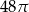48π .

Zadanie 14
(5 pkt)

Oblicz objętość czworościanu foremnego o krawędzi a .

Zadanie 15
(5 pkt)

Wysokość czworościanu foremnego ma długość 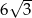√ -- 6 3 . Oblicz jego objętość i pole powierzchni całkowitej.

Zadanie 16
(5 pkt)

Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 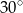30 ∘ .

Zadanie 17
(5 pkt)

Promień i wysokość walca mają jednakową długość. Pole powierzchni bocznej wynosi 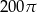200 π . Oblicz pole podstawy walca.

Zadanie 18
(5 pkt)

Wysokość czworościanu foremnego ma długość 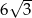√ -- 6 3 . Oblicz jego objętość i pole powierzchni całkowitej.

Arkusz Wersja PDF
Rozwiązania Edytuj w kreatorze