Zestaw użytkownika nr 6071_9831
GEOMETRIA ANALITYCZNA PCzas pracy: 90 min.Suma punktów: 70
Wykaż, że prosta 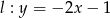 jest styczna do okręgu
jest styczna do okręgu 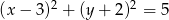 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 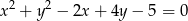 .
.
Wyznacz odległość punktu 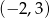 od prostej o równaniu
od prostej o równaniu 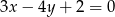 .
.
W układzie współrzędnych dane są dwa punkty: 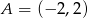 i
i 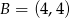 .
.
- Wyznacz równanie symetralnej odcinka
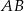 .
. - Prosta
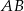 oraz prosta o równaniu
oraz prosta o równaniu 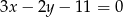 przecinają się w punkcie
przecinają się w punkcie 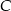 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 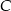 .
.
Dane są dwa przeciwległe wierzchołki kwadratu 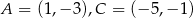 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Dane są dwa przeciwległe wierzchołki kwadratu 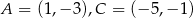 . Wyznacz obwód tego kwadratu.
. Wyznacz obwód tego kwadratu.
Dany jest jeden koniec odcinka 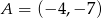 i jego środek
i jego środek 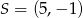 . Wyznacz współrzędne drugiego końca tego odcinka.
. Wyznacz współrzędne drugiego końca tego odcinka.
Dane są punkty 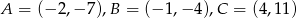 . Wykaż, że punkty te są współliniowe
. Wykaż, że punkty te są współliniowe
Określ wzajemne położenie okręgów 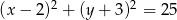 i
i 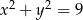 .
.
Oblicz pole i obwód trójkąta o wierzchołkach: 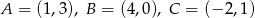 .
.
Napisz równanie okręgu o środku w punkcie 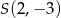 , stycznego do osi
, stycznego do osi 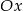 .
.
Napisz równanie wysokości trójkąta o wierzchołkach 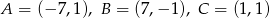 opuszczonej z wierzchołka
opuszczonej z wierzchołka 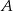 .
.
Oblicz pole trójkąta o wierzchołkach 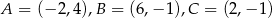 .
.
Wyznacz współrzędne punktów wspólnych prostej 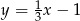 i okręgu
i okręgu 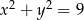 .
.
Zapisz równanie prostej przechodzącej przez punkt 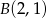 i prostopadłej do prostej danej równaniem
i prostopadłej do prostej danej równaniem 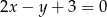 .
.
Dany jest okrąg 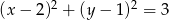 . Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
. Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.
Okrąg o równaniu 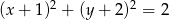 :
:
A) nie przecina osi 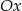 ,
,
B) nie przecina osi 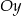 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 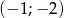 .
.
Promień okręgu o równaniu 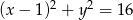 jest równy
jest równy
A) 4 B) 1 C) 3 D) 2
Środek 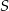 okręgu o równaniu
okręgu o równaniu 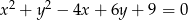 ma współrzędne
ma współrzędne
A) 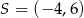 B)
B) 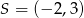 C)
C) 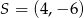 D)
D) 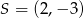
Środkiem okręgu jest punkt 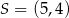 . Do okręgu należy punkt
. Do okręgu należy punkt 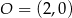 . Równanie tego okręgu to
. Równanie tego okręgu to
A) 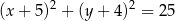
B) 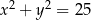
C) 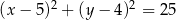
D) 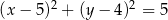
Punkt 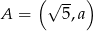 należy do prostej o równaniu
należy do prostej o równaniu 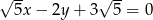 . Wynika stąd, że
. Wynika stąd, że
A) 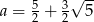 B)
B) 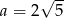 C)
C) 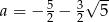 D)
D) 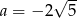
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 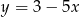 jest równy
jest równy
A) 3 B) -5 C) 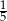 D)
D) 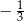
Okrąg o równaniu 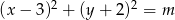 przechodzi przez punkt o współrzędnych
przechodzi przez punkt o współrzędnych 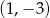 . Wtedy liczba
. Wtedy liczba 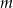 jest równa
jest równa
A) 5 B) 17 C) 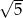 D) 25
D) 25
Pole figury ograniczonej prostymi 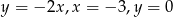 i
i 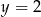 jest równe
jest równe
A) 9 B) 5 C) 19 D) 18
Odcinek o końcach 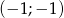 i
i 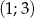 jest zawarty w prostej:
jest zawarty w prostej:
A) 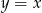 B)
B) 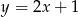 C)
C) 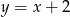 D)
D) 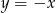
Które z podanych równań jest równaniem prostej.
A) 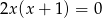 B)
B) 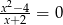 C)
C) 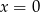 D)
D) 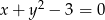
Odległość punktu 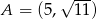 od początku układu współrzędnych jest równa
od początku układu współrzędnych jest równa
A) 6 B) 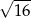 C)
C) 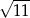 D) 5
D) 5
Dany jest okrąg o równaniu 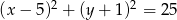 . Długość tego okręgu jest równa
. Długość tego okręgu jest równa
A) 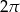 B)
B) 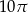 C)
C) 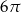 D)
D) 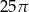
Punkty 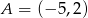 i
i 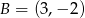 są wierzchołkami trójkąta równobocznego
są wierzchołkami trójkąta równobocznego 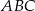 . Obwód tego trójkąta jest równy
. Obwód tego trójkąta jest równy
A) 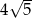 B) 30 C) 36 D)
B) 30 C) 36 D) 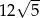
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 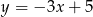 jest równy
jest równy
A) 3 B) 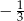 C) -3 D)
C) -3 D) 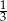
Punkty 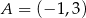 i
i 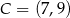 są przeciwległymi wierzchołkami prostokąta
są przeciwległymi wierzchołkami prostokąta 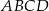 . Promień okręgu opisanego na tym prostokącie jest równy
. Promień okręgu opisanego na tym prostokącie jest równy
A) 5 B) 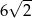 C) 10 D)
C) 10 D) 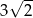
Dane są punkty 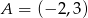 oraz
oraz 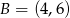 . Długość odcinka
. Długość odcinka 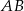 jest równa
jest równa
A) 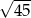 B)
B) 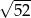 C)
C) 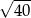 D)
D) 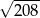
Które z równań opisuje prostą prostopadłą do prostej o równaniu 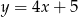 ?
?
A) 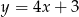 B)
B) 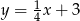 C)
C) 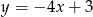 D)
D) 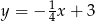
Liczba punktów wspólnych okręgu o równaniu 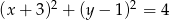 z osiami układu współrzędnych jest równa
z osiami układu współrzędnych jest równa
A) 2 B) 1 C) 0 D) 4
Punkty 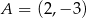 i
i 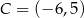 są wierzchołkami rombu
są wierzchołkami rombu 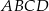 . Środkiem okręgu wpisanego w romb jest punkt
. Środkiem okręgu wpisanego w romb jest punkt
A) 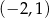 B)
B) 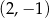 C)
C) 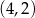 D)
D) 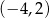
Punkty 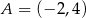 i
i 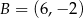 są końcami podstawy trójkąta równoramiennego
są końcami podstawy trójkąta równoramiennego 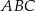 . Prosta zawierająca wysokość
. Prosta zawierająca wysokość 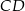 tego trójkąta przecina prostą
tego trójkąta przecina prostą 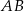 w punkcie
w punkcie
A) 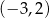 B)
B) 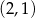 C)
C) 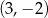 D)
D) 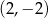
Proste o równaniach 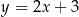 oraz
oraz 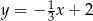
A) są prostopadłe
B) są równoległe i różne
C) przecinają się pod kątem innym niż prosty
D) pokrywają się

