Zestaw użytkownika nr 6136_7314
Zestaw użytkownika
nr 6136_7314
Ciąg 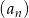 jest określony wzorem
jest określony wzorem 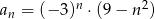 dla
dla 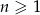 . Wynika stąd, że
. Wynika stąd, że
A) 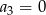 B)
B) 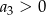 C)
C) 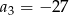 D)
D) 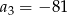
Dany jest ciąg arytmetyczny, w którym 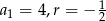 . Wtedy
. Wtedy
A) 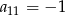 B)
B) 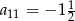 C)
C) 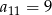 D)
D) 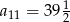
Dany jest ciąg 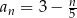 , gdzie
, gdzie 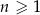 . Ten ciąg
. Ten ciąg
A) ma 15 wyrazów dodatnich
B) ma nieskończenie wiele wyrazów dodatnich
C) nie ma wyrazów dodatnich
D) ma 14 wyrazów dodatnich
Suma ciągu arytmetycznego jest określona wzorem 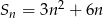 . Drugi wyraz tego ciągu jest równy
. Drugi wyraz tego ciągu jest równy
A) 2 B) 24 C) 15 D) 6
Dany jest ciąg arytmetyczny o pierwszym wyrazie 6 i różnicy 2. Wyraz ogólny ciągu wyraża się wzorem
A) 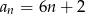 B)
B) 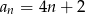 C)
C) 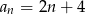 D)
D) 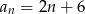
Liczby 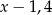 i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba
i 8 (w podanej kolejności) są pierwszym, drugim i trzecim wyrazem ciągu arytmetycznego. Wówczas liczba  jest równa
jest równa
A) 1 B) -1 C) -7 D) 3
W ciągu geometrycznym pierwszy wyraz 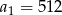 , a iloraz
, a iloraz 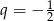 . Ósmy wyraz tego ciągu jest równy
. Ósmy wyraz tego ciągu jest równy
A) -2 B) 4 C) -4 D) 2
W ciągu geometrycznym drugi wyraz jest równy 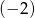 , a trzeci wyraz
, a trzeci wyraz 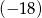 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 3 B) -3 C) 9 D) -9
Piąty wyraz ciągu 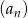 określonego wzorem
określonego wzorem 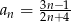 , gdzie
, gdzie 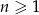 jest równy
jest równy
A) 10 B) 0,5 C) 1 D) 5
Ciąg 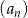 określony jest wzorem
określony jest wzorem 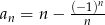 , gdzie
, gdzie 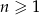 . Suma trzech początkowych wyrazów tego ciągu jest równa
. Suma trzech początkowych wyrazów tego ciągu jest równa
A) 6 B) 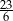 C) 7 D)
C) 7 D)