Zestaw użytkownika nr 6174_6132
próbna matura
Wskaż liczbę, której 4% jest równe 8.
A) 200 B) 100 C) 3,2 D) 32
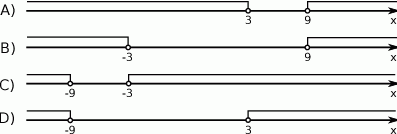
Odległość liczby  od liczby -8 na osi liczbowej jest równa
od liczby -8 na osi liczbowej jest równa
A) 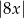 B)
B) 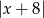 C)
C) 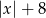 D)
D) 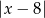
Wskaż rysunek, na którym jest przedstawiony zbiór rozwiązań nierówności 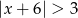 .
.
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej:
![]()
A) 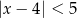 B)
B) 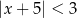 C)
C) 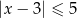 D)
D) 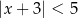
Zbiór wszystkich liczb  , których odległość od liczby
, których odległość od liczby 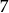 na osi liczbowej jest nie mniejsza niż
na osi liczbowej jest nie mniejsza niż 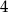 , jest opisany nierównością
, jest opisany nierównością
A) 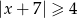 B)
B) 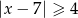 C)
C) 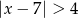 D)
D) 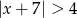
Która z liczb jest rozwiązaniem równania 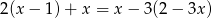 ?
?
A) 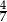 B)
B) 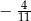 C) -1 D)
C) -1 D) 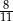
Mniejszą z dwóch liczb spełniających równanie 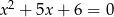 jest
jest
A) -1 B) -3 C) -2 D) -6
Liczba rozwiązań równania 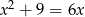 wynosi
wynosi
A) 1 B) 0 C) 3 D) 2
Równanie 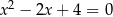
A) ma pierwiastki 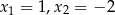
B) ma jeden pierwiastek
C) nie ma pierwiastków
D) ma pierwiastki 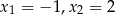
Liczby  i
i  są pierwiastkami równania
są pierwiastkami równania 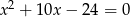 i
i 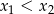 . Oblicz
. Oblicz 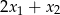 .
.
A) -22 B) 13 C) -17 D) 8
Wyróżnik 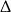 jest równy 0 dla trójmianu kwadratowego
jest równy 0 dla trójmianu kwadratowego
A) 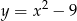 B)
B) 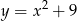 C)
C) 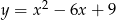 D)
D) 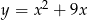
Liczba rozwiązań równania 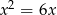 wynosi
wynosi
A) 0 B) 3 C) 2 D) 1
Rozwiązaniem równania 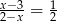 jest liczba
jest liczba
A) 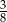 B)
B)  C)
C) 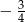 D)
D) 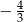
Liczba rozwiązań równania 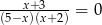 jest równa
jest równa
A) 1 B) 3 C) 0 D) 2
Powierzchnia sześcianu wynosi 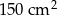 . Krawędź tego sześcianu ma długość
. Krawędź tego sześcianu ma długość
A) 5 cm B) 4 cm C) 5,5 cm D) 6 cm
Objętość sześcianu jest równa 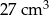 . Jaka jest suma długości wszystkich krawędzi tego sześcianu?
. Jaka jest suma długości wszystkich krawędzi tego sześcianu?
A) 24 cm B) 36 cm C) 12 cm D) 18 cm
Przekątna ściany sześcianu ma długość 8. Przekątna tego sześcianu ma długość
A) 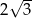 B)
B) 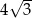 C)
C) 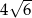 D)
D) 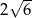
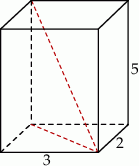
Przekątna prostopadłościanu o wymiarach 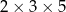 ma długość
ma długość
A) 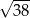 B)
B) 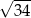 C)
C) 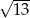 D)
D) 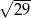
Pole powierzchni całkowitej prostopadłościanu o wymiarach 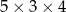 jest równe
jest równe
A) 60 B) 20 C) 94 D) 47
Przekrój osiowy walca jest kwadratem o boku długości 6. Objętość tego walca jest równa
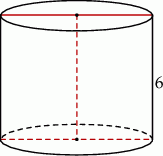
A) 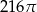 B)
B) 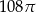 C)
C) 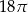 D)
D) 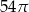
Przekrój osiowy stożka jest trójkątem równobocznym o boku długości 6.
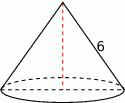
Pole powierzchni bocznej tego stożka jest równe
A) 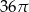 B)
B) 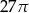 C)
C) 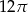 D)
D) 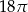
Prostą równoległą do prostej 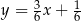 jest prosta:
jest prosta:
A) 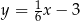 B)
B) 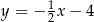 C)
C) 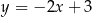 D)
D) 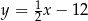
Współczynnik kierunkowy prostej równoległej do prostej o równaniu 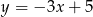 jest równy
jest równy
A) 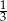 B)
B) 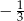 C) 3 D) -3
C) 3 D) -3
Które z równań opisuje prostą prostopadłą do prostej o równaniu 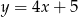 ?
?
A) 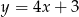 B)
B) 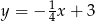 C)
C) 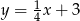 D)
D) 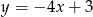
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 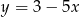 jest równy
jest równy
A) -5 B) 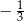 C)
C) 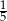 D) 3
D) 3
Rysunek przedstawia wykres funkcji 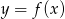 .
.
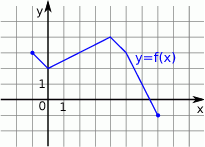
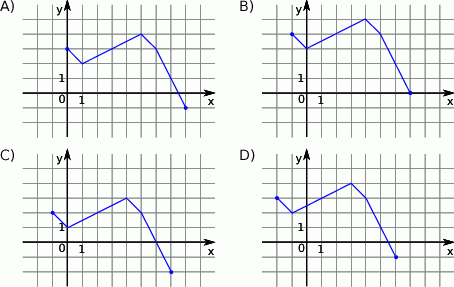
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 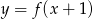 .
.
Rysunek przedstawia wykres funkcji 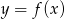 .
.
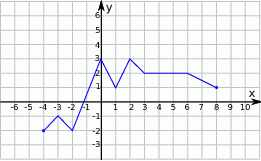
Wskaż wykres funkcji  .
.
Na rysunku 1 jest przedstawiony wykres funkcji 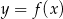 .
.
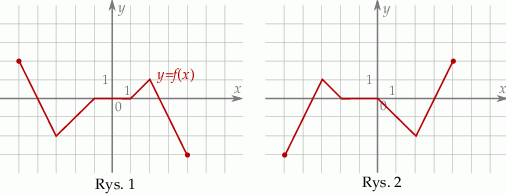
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 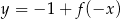 B)
B) 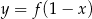 C)
C) 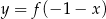 D)
D) 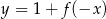
Na rysunku 1 jest przedstawiony wykres funkcji 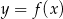 .
.
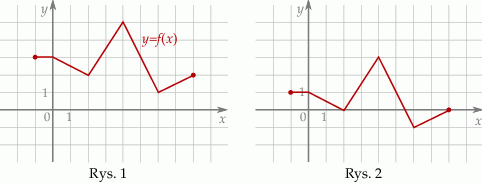
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 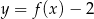 B)
B) 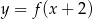 C)
C) 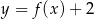 D)
D) 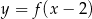
Rozwiąż równanie 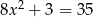 .
.
Rozwiąż równanie 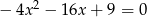 .
.
Rozwiąż równanie 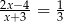 .
.
Rozwiąż równanie 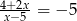 .
.
Rozwiąż równanie 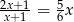 .
.
Oblicz pole trójkąta równoramiennego 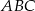 , w którym
, w którym 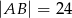 i
i 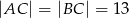 .
.
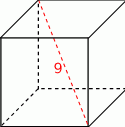
Przekątna sześcianu ma długość 9. Oblicz pole powierzchni całkowitej tego sześcianu.
Oblicz wysokość prostopadłościanu, którego podstawa jest prostokątem o wymiarach 3 i 4, a pole powierzchni całkowitej wynosi 94.
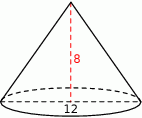
Przekrój osiowy stożka jest trójkątem równoramiennym o podstawie długości 12. Wysokość stożka jest równa 8. Oblicz pole powierzchni bocznej tego stożka.
Oblicz objętość kuli wiedząc że jej pole powierzchni jest równe 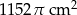 .
.
Rozwiąż nierówność 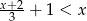 .
.

