Zestaw użytkownika nr 6183_9084
Zestaw użytkownika
nr 6183_9084
W pojemniku o kształcie walca o promieniu podstawy 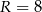 umieszczono dwie kule o promieniu
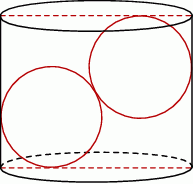
umieszczono dwie kule o promieniu 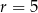 , w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
, w ten sposób, że są do siebie styczne i każda z nich dotyka powierzchni bocznej walca, jak na rysunku. Jaka co najmniej musi być wysokość pojemnika, aby kule całkowicie się w nim mieściły. Oblicz objętość tego walca.
Do naczynia w kształcie walca wypełnionego wodą do wysokości 7 cm włożono metalową kulkę o promieniu 3 cm. Poziom wody podniósł się o 1 cm i zrównał się z górną podstawą walca. Oblicz objętość naczynia. Przyjmując 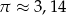 , wynik podaj z dokładnością do
, wynik podaj z dokładnością do 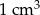 .
.
Powierzchnia boczna stożka jest wycinkiem kołowym, którego kąt środkowy ma miarę 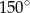 . Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
. Wiedząc, że tworząca stożka ma długość 24 cm, oblicz pole powierzchni bocznej i objętość tego stożka.
Oblicz objętość stożka, którego tworząca o długości 4 jest nachylona do płaszczyzny podstawy pod kątem 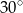 .
.
Przekrój stożka wyznaczony przez wierzchołek i cięciwę podstawy jest trójkątem równobocznym, o polu równym 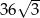 . Płaszczyzna
. Płaszczyzna  , do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej
, do której należy ten przekrój, tworzy z płaszczyzną podstawy stożka kąt o mierze równej 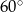 . Oblicz objętość stożka.
. Oblicz objętość stożka.

