Zestaw użytkownika nr 6221_1290
TEST 2
Dwudziestu sześciu uczniów klasy gimnazjalnej postanowiło wybrać się na czterodniową wycieczkę z trzema noclegami. Trasa przejazdu wynosiła łącznie 600 km. W biurze turystycznym uczniowie otrzymali następujące propozycje:
– cena jednego noclegu – 25 zł od osoby
– wyżywienie w ciągu jednego dnia (śniadanie, obiad, kolacja) – 30 zł od osoby
– bilety wejściowe do muzeum i przewodnik grupy dla całej wycieczki – 1200 zł
– cena 1 km przejazdu autokarem – 2,50 zł
Oblicz łączny koszt wycieczki dla całej grupy, jeśli pierwszego dnia uczniowie mają zamiar skorzystać tylko z obiadu i kolacji, czwartego dnia tylko ze śniadania. Oblicz koszt wycieczki na jednego ucznia.
Beczka ma pojemność 67,2 litra, dzbanek - 1,6 litra, a kubek ma pojemność 5 razy mniejszą niż dzbanek. Napełnienie dzbanka wodą z kranu trwa 20 s, pokonanie drogi od kranu do beczki trwa 10 s i tyle samo trwa powrót do kranu. Wylewanie wody z dzbanka trwa 5 s.
- Ile czasu zajmie napełnienie beczki wodą za pomocą dzbanka?
- Ile czasu zajęłoby napełnienie beczki wodą za pomocą kubka? Przyjmijmy, że dojście do beczki i powrót do kranu z kubkiem w ręku trwa tyle samo, co z dzbankiem.
W obu sytuacjach należy przyjąć, że na początku i na końcu stoimy przy beczce.
W fabryce zabawek znajduje się 10 maszyn do produkcji plastikowych samochodów. Średnia wydajność jednej maszyny wynosi 2100 samochodów dziennie. W okresie przedświątecznym uruchomiono jedną dodatkową maszynę, w wyniku czego średnia dzienna wydajność pojedynczego urządzenia zmalała o 4%. Oblicz ile samochodów dziennie produkuje dodatkowa maszyna.
Gdyby Aleksander Wielki umarł o 5 lat wcześniej, to panowałby przez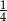 
swego życia. Gdyby żył o 9 lat dłużej, to panowałby przez połowę swego życia. Ile lat żył i ile lat panował.
W pewnej szkole 40 uczniów to członkowie SKS-u. Wśród nich 26 gra w siatkówkę, 25 pływa, a 27 jeździ na nartach. Jednocześnie pływa i gra w siatkówkę 15 uczniów, gra w siatkówkę i jeździ na nartach 16, a pływa i jeździ na nartach 18. Jeden uczeń nie zajmuje się sportem. Ilu uczniów uprawia wszystkie trzy dyscypliny sportowe? Ilu uczniów uprawia tylko jedną dyscyplinę sportową?
Z kwadratowego kawałka materiału o boku 1,6 m wykonano obrus. Na brzegi obrusa naszyto ozdobną taśmę. Taką samą taśmę naszyto również na powierzchnię obrusa, tworząc wzór w następujący sposób.
- Każdy bok obrusa podzielono dwoma punktami na odcinki, których długości mają się do siebie jak 1:2:1.
- Ozdobną taśmą łączono co drugi z wyznaczonych punktów. Powstały dwa czworokąty.
Oblicz, ile taśmy zużyto na ozdobienie obrusa, jeżeli dodatkowo na szwy przeznaczono 15 cm tej taśmy. Wynik podaj z dokładnością do 0,1 m.
Udowodnij, że przekątna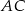 
kwadratu 
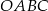jest równa przekątnej 
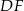prostokąta 
.
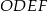W sześciokącie foremnym połączono środki sąsiednich boków otrzymując ponownie sześciokąt foremny. Oblicz stosunek pól: otrzymanego i wyjściowego sześciokąta.
