Zestaw użytkownika nr 6255_9871
Zestaw użytkownika
nr 6255_9871
Dany jest ciąg arytmetyczny 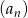 dla
dla 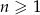 , w którym
, w którym 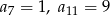 .
.
- Oblicz pierwszy wyraz
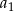 i różnicę
i różnicę  ciągu
ciągu 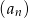 .
. - Sprawdź, czy ciąg
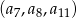 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 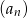 miała wartość najmniejszą.
miała wartość najmniejszą.
Ciąg 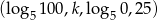 jest arytmetyczny. Wobec tego
jest arytmetyczny. Wobec tego
A) 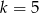 B)
B) 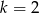 C)
C) 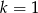 D)
D) 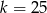
W ciągu arytmetycznym 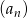 wyraz
wyraz 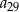 jest dwa razy większy od wyrazu
jest dwa razy większy od wyrazu 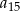 oraz
oraz 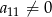 . Wtedy iloraz
. Wtedy iloraz 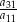 jest równy
jest równy
A) 3 B) 1 C) 2 D) 4
Ciąg 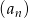 , gdzie
, gdzie 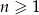 , jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji
, jest rosnącym ciągiem geometrycznym. Wyznacz największą wartość funkcji 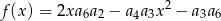 .
.
Długości boków trójkąta tworzą ciąg geometryczny. Jaki warunek spełniać musi iloraz tego ciągu?
Dla jakich wartości  liczby
liczby 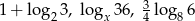 są kolejnymi wyrazami ciągu geometrycznego.
są kolejnymi wyrazami ciągu geometrycznego.
Trzy liczby są kolejnymi wyrazami ciągu arytmetycznego. Ich suma wynosi 18. Jeśli największą z tych liczb zwiększymy o 8, a pozostałych nie zmienimy, to uzyskamy trzy kolejne wyrazy ciągu geometrycznego. Wyznacz te liczby.
Liczba  jest pierwszym wyrazem ciągu geometrycznego
jest pierwszym wyrazem ciągu geometrycznego 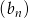 , którego iloraz jest równy
, którego iloraz jest równy 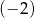 . Pierwszy wyraz ciągu arytmetycznego
. Pierwszy wyraz ciągu arytmetycznego 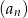 jest taki sam jak pierwszy wyraz ciągu
jest taki sam jak pierwszy wyraz ciągu 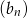 . Suma siedmiu początkowych wyrazów ciągu
. Suma siedmiu początkowych wyrazów ciągu 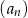 jest równa sumie siedmiu początkowych wyrazów ciągu
jest równa sumie siedmiu początkowych wyrazów ciągu 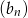 . Oblicz różnicę ciągu arytmetycznego
. Oblicz różnicę ciągu arytmetycznego 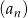 .
.
Ciąg 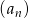 określony jest rekurencyjnie:
określony jest rekurencyjnie: 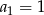 ,
, 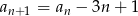 dla
dla 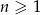 .
.
- Oblicz 4 wyraz ciągu
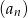 .
. - Zbadaj monotoniczność ciągu
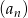 .
.

