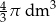Zestaw użytkownika nr 6321_2035
Zestaw użytkownika
nr 6321_2035
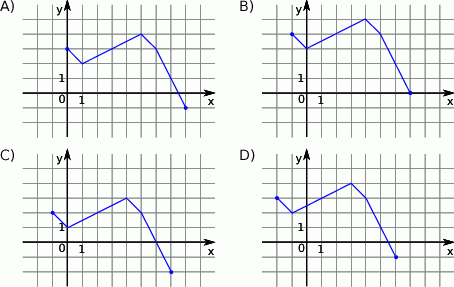
Rozwiąż nierówność 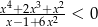 .
.
Na rysunku przedstawiony jest wykres funkcji  określonej wzorem
określonej wzorem 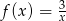 dla
dla 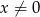 .
.
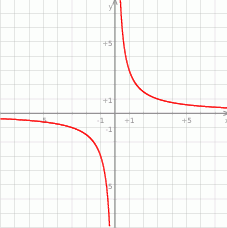
Wykres ten przesunięto o 2 jednostki w górę wzdłuż osi 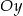 . Otrzymano w ten sposób wykres funkcji
. Otrzymano w ten sposób wykres funkcji 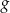 o wzorze
o wzorze 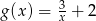 dla
dla 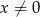 .
.
- Narysuj wykres funkcji
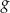 .
. - Oblicz największą wartość funkcji
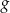 w przedziale
w przedziale 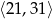 .
. - Podaj, o ile jednostek wzdłuż osi
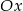 należy przesunąć wykres funkcji
należy przesunąć wykres funkcji 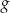 , aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
, aby otrzymać wykres funkcji przechodzący przez początek układu współrzędnych.
Okrąg o równaniu 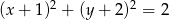 :
:
A) nie przecina osi 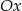 ,
,
B) nie przecina osi 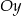 ,
,
C) przechodzi przez początek układu współrzędnych,
D) przechodzi przez punkt 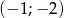 .
.
Wyrażenie 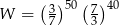 jest równe
jest równe
A) 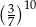 B)
B) 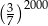 C) 1 D)
C) 1 D) 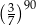
Znajdź wszystkie liczby całkowite spełniające nierówność 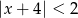 .
.
Stosunek miar kątów czworokąta jest równy 1:2:3:4. Zatem najmniejszy kąt tego wielokąta ma miarę
A) 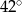 B)
B) 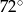 C)
C) 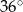 D)
D) 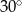
Rozwiąż równanie 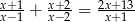 .
.
Wskaż 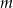 , dla którego funkcja liniowa
, dla którego funkcja liniowa 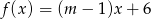 jest rosnąca
jest rosnąca
A) 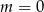 B)
B) 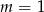 C)
C) 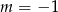 D)
D) 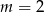
Promień okręgu o równaniu 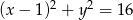 jest równy
jest równy
A) 1 B) 2 C) 4 D) 3
Na rysunku jest przedstawiony wykres funkcji 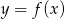 .
.
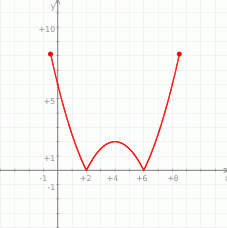
Które równanie ma dokładnie trzy rozwiązania?
A) 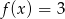 B)
B) 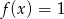 C)
C) 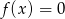 D)
D) 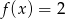
Odwrotność liczby będącej rozwiązaniem równania 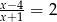 jest równa
jest równa
A) 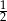 B)
B) 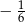 C) 6 D)
C) 6 D) 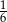
Napisz wzór funkcji liniowej o współczynniku kierunkowym 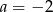 , której wykres przecina oś
, której wykres przecina oś 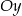 w punkcie
w punkcie 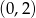 . Wyznacz miejsce zerowe tej funkcji.
. Wyznacz miejsce zerowe tej funkcji.
Rozwiąż układ równań:
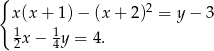
Liczba 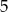 nie należy do dziedziny wyrażenia
nie należy do dziedziny wyrażenia
A) 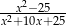 B)
B) 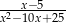 C)
C) 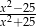 D)
D) 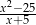
Znajdź  , dla którego liczby
, dla którego liczby 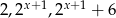 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.
Wyrażenie 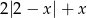 dla
dla 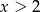 ma wartość
ma wartość
A) 5 B) 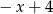 C) 1 D)
C) 1 D) 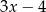
Wskaż liczbę, której 4% jest równe 8.
A) 200 B) 3,2 C) 32 D) 100
Wyznacz wszystkie rozwiązania równania 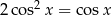 należące do przedziału
należące do przedziału 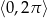 .
.
Mniejszą z dwóch liczb spełniających równanie 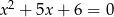 jest
jest
A) -3 B) -2 C) -6 D) -1
Liczbę 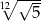 można zapisać inaczej w postaci
można zapisać inaczej w postaci
A) 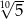 B)
B) 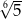 C)
C) 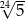 D)
D) 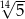
Na seans filmowy sprzedano 280 biletów, w tym 126 ulgowych. Jaki procent sprzedanych biletów stanowiły bilety ulgowe?
A) 63% B) 45% C) 22% D) 33%
Określ dziedzinę funkcji 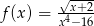 .
.
Wyznacz równanie prostej przechodzącej przez początek układu współrzędnych i przez środek okręgu o równaniu 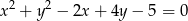 .
.
Dane są wielomiany 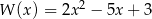 i
i 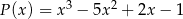 . Wielomian
. Wielomian 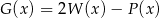 jest równy
jest równy
A) 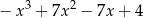 B)
B) 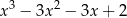 C)
C) 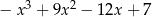 D)
D) 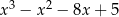
Pierwiastkami wielomianu stopnia trzeciego 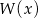 są liczby
są liczby 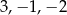 , a współczynnik stojący przy najwyższej potędze zmiennej
, a współczynnik stojący przy najwyższej potędze zmiennej  jest równy 3. Wielomian ten można zapisać w postaci
jest równy 3. Wielomian ten można zapisać w postaci
A) 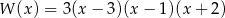
B) 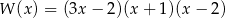
C) 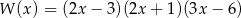
D) 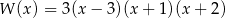
Odległość liczby  od liczby -8 na osi liczbowej jest równa
od liczby -8 na osi liczbowej jest równa
A) 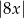 B)
B) 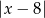 C)
C) 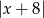 D)
D) 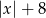
Rozwiąż równanie 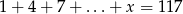 .
.
Funkcje 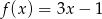 i
i 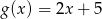 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 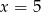 B)
B) 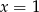 C)
C) 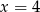 D)
D) 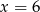
Za 4 lata Ula będzie miała dwa razy więcej lat niż miała 2 lata temu. Ile lat ma Ula?
Rysunek przedstawia wykres funkcji 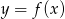 .
.
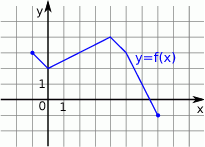
Wskaż rysunek, na którym przedstawiony jest wykres funkcji 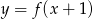 .
.
Rozwiąż równanie 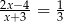 .
.
Do wykresu funkcji  nie należy punkt
nie należy punkt
A) 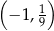 B)
B) 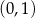 C)
C) 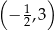 D)
D) 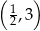
Liczba 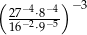 jest równa
jest równa
A) 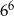 B)
B) 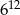 C)
C) 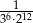 D)
D) 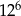
Uprość wyrażenie 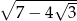 .
.
Dziedziną funkcji 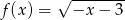 jest zbiór
jest zbiór
A) 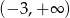 B)
B) 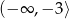 C)
C) 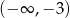 D)
D) 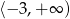
Średnią arytmetyczną licz 5,5,7,3,9,9,4,4 jest liczba
A) 5,75 B) 4 C) 8 D) 5,5
Dla jakich wartości parametru 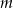 suma odwrotności pierwiastków równania
suma odwrotności pierwiastków równania 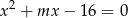 jest równa -4?
jest równa -4?
Liczba rozwiązań równania 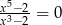 jest równa
jest równa
A) 5 B) 1 C) 0 D) 2
Wskaż funkcję, która nie przyjmuje wartości ujemnych
A) 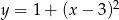 B)
B) 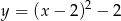 C)
C) 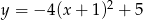 D)
D) 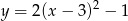
Objętość kuli o promieniu 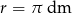 jest równa
jest równa
A) 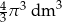 B)
B) 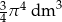 C)
C) 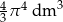 D)
D)