Zestaw użytkownika nr 6343_1733
Zestaw użytkownika
nr 6343_1733
Suma drugiego, czwartego i szóstego wyrazu ciągu arytmetycznego jest równa 42, zaś suma kwadratów wyrazów drugiego i trzeciego jest równa 185. Wyznacz pierwszy wyraz i różnicę tego ciągu.
Dany jest ciąg arytmetyczny 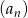 dla
dla 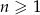 , w którym
, w którym 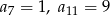 .
.
- Oblicz pierwszy wyraz
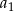 i różnicę
i różnicę  ciągu
ciągu 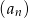 .
. - Sprawdź, czy ciąg
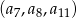 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 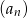 miała wartość najmniejszą.
miała wartość najmniejszą.
Podaj wzór na wyraz ogólny ciągu 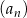 określonego w następujący sposób: ciąg
określonego w następujący sposób: ciąg 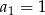 jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
Znajdź  , dla którego liczby
, dla którego liczby 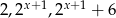 w podanej kolejności tworzą ciąg arytmetyczny.
w podanej kolejności tworzą ciąg arytmetyczny.
Dany jest ciąg 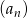 mający tę własność, że dla każdej liczby naturalnej
mający tę własność, że dla każdej liczby naturalnej  suma
suma  początkowych wyrazów tego ciągu jest równa
początkowych wyrazów tego ciągu jest równa 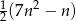 . Oblicz dwudziesty wyraz tego ciągu. Wykaż, że
. Oblicz dwudziesty wyraz tego ciągu. Wykaż, że 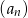 jest ciągiem arytmetycznym.
jest ciągiem arytmetycznym.
Cztery liczby tworzą ciąg geometryczny. Wyznacz te liczby wiedząc, że suma pierwszej i czwartej wynosi 36, a suma drugiej i trzeciej liczby wynosi 24.
Dany jest ciąg o wyrazie ogólnym 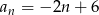 . Wybierz sto kolejnych początkowych wyrazów ciągu
. Wybierz sto kolejnych początkowych wyrazów ciągu 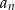 i oblicz dla jakiej liczby naturalnej
i oblicz dla jakiej liczby naturalnej 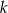 stosunek wyrazu stojącego na miejscu
stosunek wyrazu stojącego na miejscu 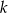 , licząc od początku, do wyrazu stojącego na miejscu
, licząc od początku, do wyrazu stojącego na miejscu 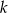 , licząc od końca, jest równy
, licząc od końca, jest równy 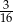 .
.
Suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 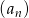 wyraża się wzorem
wyraża się wzorem 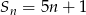 . Wyznacz wzór na
. Wyznacz wzór na  -ty wyraz ciągu
-ty wyraz ciągu 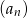 dla
dla 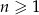 .
.
Suma trzech początkowych wyrazów ciągu geometrycznego wynosi 26, różnica wyrazów czwartego i pierwszego wynosi 52. Oblicz piąty wyraz tego ciągu.
Suma dziewięciu początkowych wyrazów ciągu arytmetycznego wynosi 18, a suma siedmiu początkowych wyrazów jest równa 0. Wyrazy: siódmy, ósmy i dziewiąty są długościami boków trójkąta. Oblicz stosunek długości promienia okręgu wpisanego w ten trójkąt do długości promienia okręgu na nim opisanego.
Suma trzech początkowych wyrazów nieskończonego ciągu geometrycznego wynosi 6, a suma 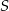 wszystkich wyrazów tego ciągu jest równa
wszystkich wyrazów tego ciągu jest równa 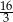 . Dla jakich naturalnych
. Dla jakich naturalnych  spełniona jest nierówność
spełniona jest nierówność 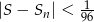 ?
?
Rozwiąż układ równań:
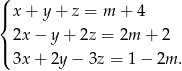
Dla jakich wartości parametru 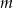 liczby
liczby 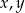 i
i  są kolejnymi wyrazami ciągu geometrycznego?
są kolejnymi wyrazami ciągu geometrycznego?
Dany jest ciąg arytmetyczny 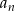 w którym
w którym 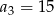 oraz
oraz 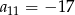 .
.
- Dla jakich
 zachodzi równość
zachodzi równość 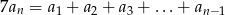 ?
? - Oblicz sumę pięćdziesięciu początkowych, ujemnych wyrazów ciągu
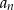 , które są podzielne przez 3.
, które są podzielne przez 3.
Liczby 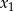 i
i 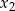 są pierwiastkami równania
są pierwiastkami równania 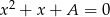 , a liczby
, a liczby 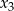 i
i 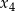 są pierwiastkami równania
są pierwiastkami równania 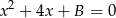 . Wiadomo, że ciąg
. Wiadomo, że ciąg 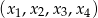 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 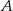 i
i 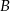 .
.

