Zestaw użytkownika nr 6343_4530
Zestaw użytkownika
nr 6343_4530
Zadanie 1
Wyznacz te wartości parametru 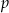 , dla których równanie
, dla których równanie 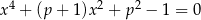 ma dokładnie dwa różne pierwiastki.
ma dokładnie dwa różne pierwiastki.
Zadanie 2
Dla jakich wartości parametru 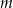 równanie
równanie 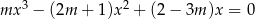 ma rozwiązania, których suma jest dodatnia?
ma rozwiązania, których suma jest dodatnia?
Zadanie 3
Rozwiąż równanie 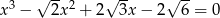 .
.
Zadanie 4
Dany jest wielomian 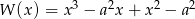 , gdzie
, gdzie 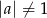 .
.
- Oblicz sumę pierwiastków tego wielomianu.
- Wyznacz wartość parametru
 , dla której suma kwadratów pierwiastków wielomianu
, dla której suma kwadratów pierwiastków wielomianu 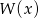 jest możliwie najmniejsza.
jest możliwie najmniejsza.
Zadanie 5
Rozwiąż równanie
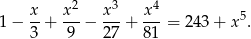
Zadanie 6
Pierwiastkami wielomianu 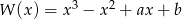 są tylko dwie liczby: 2 oraz (-3).
są tylko dwie liczby: 2 oraz (-3).
- Oblicz
 i
i 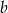 .
. - Zapisz wielomian w postaci czynników liniowych.
Zadanie 7
Dany jest wielomian 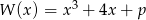 , gdzie
, gdzie 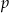 jest liczbą pierwszą. Wyznacz
jest liczbą pierwszą. Wyznacz 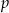 wiedząc, że
wiedząc, że 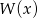 ma pierwiastek całkowity.
ma pierwiastek całkowity.
Zadanie 8
Rozwiąż równanie 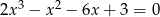 .
.

