Zestaw użytkownika nr 6507_8969
Zestaw użytkownika
nr 6507_8969
Zadanie 1
Dany jest ciąg arytmetyczny 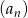 dla
dla 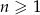 , w którym
, w którym 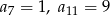 .
.
- Oblicz pierwszy wyraz
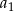 i różnicę
i różnicę  ciągu
ciągu 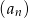 .
. - Sprawdź, czy ciąg
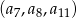 jest geometryczny.
jest geometryczny. - Wyznacz takie
 , aby suma
, aby suma  początkowych wyrazów ciągu
początkowych wyrazów ciągu 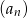 miała wartość najmniejszą.
miała wartość najmniejszą.
Zadanie 2
Podaj wzór na wyraz ogólny ciągu 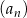 określonego w następujący sposób: ciąg
określonego w następujący sposób: ciąg 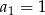 jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
jest ciągiem kolejnych liczb naturalnych, które przy dzieleniu przez 5 dają resztę 1.
Zadanie 3
Liczby 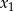 i
i 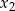 są pierwiastkami równania
są pierwiastkami równania 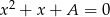 , a liczby
, a liczby 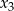 i
i 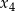 są pierwiastkami równania
są pierwiastkami równania 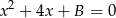 . Wiadomo, że ciąg
. Wiadomo, że ciąg 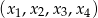 jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz
jest ciągiem geometrycznym o wyrazach całkowitych. Wyznacz 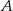 i
i 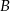 .
.
Zadanie 4
Długości boków trójkąta są kolejnymi wyrazami rosnącego ciągu geometrycznego o ilorazie 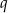 , a cosinus jednego z jego kątów jest równy
, a cosinus jednego z jego kątów jest równy 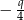 .
.
- Wyznacz
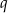 .
. - Wiedząc, że promień okręgu opisanego na tym trójkącie ma długość
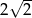 , oblicz pole tego trójkąta.
, oblicz pole tego trójkąta.

