Zestaw użytkownika nr 6520_3507
Zadania utrwalające własności funkcji liniowej (podstawa)Czas pracy: 45 min.
Wskaż 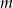 , dla którego funkcja liniowa
, dla którego funkcja liniowa 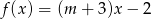 jest malejąca
jest malejąca
A) 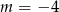 B)
B) 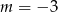 C)
C) 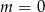 D)
D) 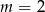
Funkcje 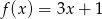 i
i 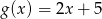 przyjmują równą wartość dla
przyjmują równą wartość dla
A) 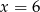 B)
B) 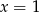 C)
C) 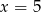 D)
D) 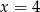
Funkcja 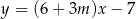 jest rosnąca, gdy
jest rosnąca, gdy
A) 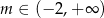 B)
B) 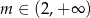 C)
C) 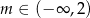 D)
D) 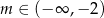
Dana jest funkcja 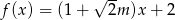 . Funkcja ta jest malejąca dla
. Funkcja ta jest malejąca dla
A) 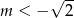 B)
B) 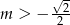 C)
C) 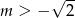 D)
D) 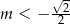
Funkcją rosnącą jest funkcja
A) 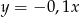 B)
B) 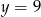 C)
C) 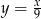 D)
D) 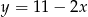
Prosta 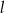 ma równanie
ma równanie 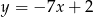 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 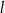 i przechodzącej przez punkt
i przechodzącej przez punkt 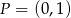 ma postać
ma postać
A) 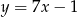 B)
B) 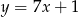 C)
C) 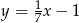 D)
D) 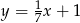
Punkt 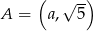 należy do prostej o równaniu
należy do prostej o równaniu 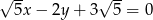 . Wynika stąd, że
. Wynika stąd, że
A) 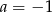 B)
B) 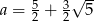 C)
C) 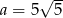 D)
D) 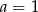
Współczynnik kierunkowy prostej prostopadłej do prostej określonej wzorem 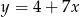 jest równy
jest równy
A) 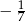 B) 7 C)
B) 7 C) 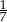 D)
D) 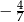
Punkt 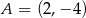 jest wierzchołkiem trapezu
jest wierzchołkiem trapezu 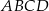 . Prosta o równaniu
. Prosta o równaniu 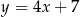 zawiera podstawę
zawiera podstawę 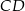 . Podstawa
. Podstawa 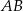 zawiera się w prostej o równaniu
zawiera się w prostej o równaniu
A) 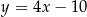 B)
B) 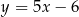 C)
C) 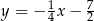 D)
D) 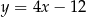
Prosta 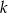 ma równanie
ma równanie 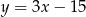 . Wskaż równanie prostej prostopadłej do
. Wskaż równanie prostej prostopadłej do 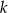 .
.
A) 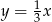 B)
B) 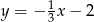 C)
C) 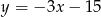 D)
D) 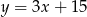
Proste o równaniach 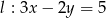 i
i 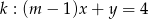 są równoległe. Wynika stąd, że
są równoległe. Wynika stąd, że
A) 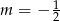 B)
B) 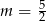 C)
C) 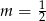 D)
D) 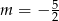
Prosta o równaniu 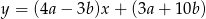 przecina oś
przecina oś 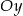 w punkcie
w punkcie 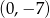 . Wtedy
. Wtedy
A) 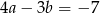 B)
B) 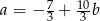 C)
C) 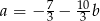 D)
D) 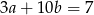
Prosta o równaniu 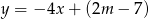 przechodzi przez punkt
przechodzi przez punkt 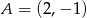 . Wtedy
. Wtedy
A) 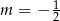 B)
B) 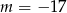 C)
C) 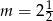 D)
D) 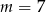
Proste o równaniach 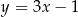 oraz
oraz 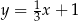
A) są równoległe i różne
B) są prostopadłe
C) przecinają się pod kątem innym niż prosty
D) pokrywają się
Wyznacz wzór funkcji liniowej 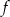 , wiedząc że nie przyjmuje ona wartości dodatnich oraz
, wiedząc że nie przyjmuje ona wartości dodatnich oraz 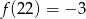 .
.
Wyznacz równanie prostej przechodzącej przez punkty 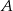 i
i 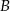 jeżeli
jeżeli 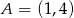 i
i 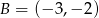 .
.
Wyznacz równanie prostej równoległej do prostej 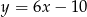 przechodzącej przez punkt
przechodzącej przez punkt 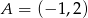 oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt
oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt 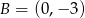 .
.

