Zestaw użytkownika nr 6597_9551
Kombinatoryka
Pan Tomasz ma 5 marynarek, 9 par różnych spodni i 6 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 45 B) 270 C) 20 D) 280
Pan Jakub ma 4 marynarki, 7 par różnych spodni i 10 różnych koszul. Na ile różnych sposobów może się ubrać, jeśli zawsze zakłada marynarkę, spodnie i koszulę.
A) 70 B) 21 C) 28 D) 280
Pan Eugeniusz szykując się rano do pracy wybiera jeden spośród swoich 12 zegarków oraz dwa spośród 22 wiecznych piór, przy czym jedno z nich traktuje jako pióro zapasowe. Na ile sposobów może wybrać zestaw składający się z zegarka i dwóch piór, głównego i zapasowego?
A) 2777 B) 34 C) 5544 D) 5808
Ile jest liczb naturalnych dwucyfrowych większych od 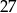 , które mają dwie różne cyfry?
, które mają dwie różne cyfry?
A) 63 B) 72 C) 65 D) 18
Ile jest wszystkich liczb naturalnych dwucyfrowych, w których obie cyfry są parzyste?
A) 24 B) 20 C) 25 D) 16
Wszystkich liczb naturalnych dwucyfrowych, których obie cyfry są mniejsze od 5 jest
A) 20 B) 25 C) 16 D) 30
Ośmiu znajomych, wśród których jest jedno małżeństwo, kupiło bilety do kina na kolejne miejsca w jednym rzędzie (w rzędzie było dokładnie 8 miejsc). Wszystkich możliwych sposobów zajęcia miejsc tak, aby małżonkowie siedzieli obok siebie, jest:
A) 5040 B) 40320 C) 10080 D) 720
W kolejce do kasy biletowej ustawiły się cztery dziewczynki i pięciu chłopców. Liczba wszystkich możliwych ustawień osób w tej kolejce wynosi
A) 9! B) 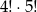 C) 4!+5! D)
C) 4!+5! D) 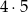
Na ile sposobów można ustawić na półce 5 tomów encyklopedii tak, aby tomy 3 i 4 stały obok siebie (w dowolnej kolejności)?
A) 48 B) 120 C) 60 D) 24
Wybieramy jedną liczbę ze zbioru 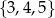 i jedną liczbę ze zbioru
i jedną liczbę ze zbioru 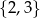 . Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
. Na ile sposobów można wybrać te liczby tak, aby ich suma była liczbą nieparzystą?
A) 4 B) 6 C) 5 D) 3
Na ile sposobów można włożyć dwie skarpetki do czterech szuflad?
A) 256 B) 32 C) 16 D) 8
Wybieramy liczbę  ze zbioru
ze zbioru 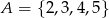 oraz liczbę
oraz liczbę 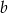 ze zbioru
ze zbioru 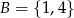 . Ile jest takich par
. Ile jest takich par 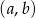 , że iloczyn
, że iloczyn 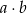 jest liczbą nieparzystą?
jest liczbą nieparzystą?
A) 20 B) 5 C) 3 D) 2
Wszystkie ściany sześcianu pomalowano. Następnie sześcian rozcięto na 64 jednakowe sześcianiki. Ile sześcianików ma pomalowaną co najmniej jedną ścianę?
A) 60 B) 63 C) 37 D) 56
Trzech panów i  pań można ustawić w jednym rzędzie na 12 sposobów, tak aby osoby tej samej płci nie stały obok siebie. Liczba
pań można ustawić w jednym rzędzie na 12 sposobów, tak aby osoby tej samej płci nie stały obok siebie. Liczba  pań jest równa
pań jest równa
A) 4 B) 8 C) 2 D) 5
Na regale można ustawić  książek na 24 sposoby. Zatem
książek na 24 sposoby. Zatem
A) 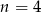 B)
B) 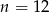 C)
C) 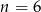 D)
D) 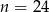
Do pomieszczenia wchodzi grupa osób składająca się z 5 kobiet i 4 mężczyzn. Pierwsze wchodzą kobiety, a za nimi mężczyźni. Liczba wszystkich możliwych sposobów takiego wejścia osób do pomieszczenia jest równa
A) 9 B) 144 C) 20 D) 2880
Ile liczb o różnych cyfrach i większych od 6000 można utworzyć z cyfr 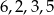 ?
?
A) 18 B) 30 C) 24 D) 6
Ile można utworzyć liczb czterocyfrowych podzielnych przez 20, o cyfrach należących do zbioru 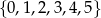 ?
?
A) 90 B) 20 C) 60 D) 12
Wybieramy liczbę  ze zbioru
ze zbioru 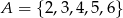 oraz liczbę
oraz liczbę 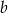 ze zbioru
ze zbioru 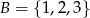 . Ile jest takich par
. Ile jest takich par 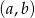 , że iloczyn
, że iloczyn 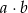 jest liczbą parzystą?
jest liczbą parzystą?
A) 5 B) 21 C) 11 D) 9
W karcie dań jest 5 zup i 4 drugie dania. Na ile sposobów można zamówić obiad składający się z jednej zupy i jednego drugiego dania?
A) 16 B) 9 C) 20 D) 25
Liczba punktów, których pierwsza współrzędna należy do zbiory 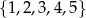 , a druga do zbioru
, a druga do zbioru 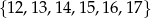 jest równa
jest równa
A) 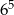 B)
B) 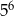 C) 30 D) 11
C) 30 D) 11
Liczba sposobów, na jakie Ala i Bartek mogą usiąść na dwóch spośród pięciu miejsc w kinie, jest równa
A) 25 B) 12 C) 15 D) 20
Na pierwszym polu 64-polowej szachownicy kładziemy jedno ziarnko maku, na drugim dwa ziarnka maku, na trzecim dwa razy więcej niż na drugim, na czwartym dwa razy więcej niż na trzecim itd. Ile ziarenek maku położymy w sumie na szachownicy?
A) 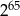 B)
B) 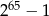 C)
C) 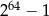 D)
D) 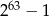
Ośmiocyfrowe numery telefonów w pewnym mieście są tworzone z cyfr 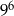 przy czym numery nie mogą zaczynać się od cyfr 0,9. Ile najwięcej takich numerów telefonicznych można utworzyć?
przy czym numery nie mogą zaczynać się od cyfr 0,9. Ile najwięcej takich numerów telefonicznych można utworzyć?
A) 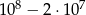 B)
B) 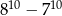 C)
C) 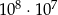 D)
D) 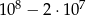
Ile jest liczb naturalnych czterocyfrowych o sumie cyfr równej 2?
A) 3 B) 2 C) 1 D) 4
Pięć spośród sześciu różnokolorowych kul wkładamy do pięciu ponumerowanych szuflad tak, że w każdej szufladzie znajduje się jedna kula. Na ile różnych sposobów można to zrobić?
A) 24 B) 720 C) 120 D) 126
Zamawiając pizzę mamy do wyboru 12 dodatków, 2 rodzaje ciasta i 3 rodzaje sosów. Na ile sposobów możemy zamówić pizzę jeżeli zdecydowaliśmy się wybrać jeden dodatek główny i jeden dodatek pomocniczy (różny od głównego), oraz jeden sos?
A) 792 B) 29 C) 864 D) 28
Ile jest liczb naturalnych trzycyfrowych, których kolejne cyfry tworzą ciąg geometryczny o ilorazie równym 2 lub 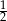 ?
?
A) 16 B) 9 C) 8 D) 4

